
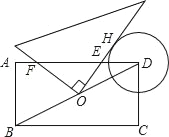
【题目】如图,在矩形ABCD中,AB=2,BC=4,⊙D的半径为1.现将一个直角三角板的直角顶点与矩形的对称中心O重合,绕着O点转动三角板,使它的一条直角边与⊙D切于点H,此时两直角边与AD交于E,F两点,则tan∠EFO的值为_____.
【答案】![]()
【解析】分析: 本题可以通过证明∠EFO=∠HDE,再求出∠HDE的正切值就是∠EFO的正切值.
详解: 连接DH,作OG⊥CD于G,如图,
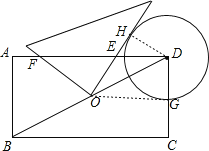
∵在矩形ABCD中,AB=2,BC=4,
∴BD=![]() =2
=2![]() ,
,
∵O是对称中心,
∴OD=![]() BD=
BD=![]() ,
,
∵OG⊥CD,
∴DG=![]() CD=1,OG=
CD=1,OG=![]() BC=2,
BC=2,
∴OG为O的切线,
∵OH是D的切线,
∴DH⊥OH,OH=OG=2,
∵DH=1,
∴tan∠ADB=![]() =
=![]() ,tan∠HOD=
,tan∠HOD=![]() =
=![]() ,
,
∵∠ADB=∠HOD,
∴OE=ED,
设EH为x,则ED=OE=OHEH=2x,
∴1 +x =(2x) ,解得x=![]() ,
,
即EH=![]() .
.
又∵∠FOE=∠DHO=90°,
∴FO∥DH,
∴∠EFO=∠HDE,
∴tan∠EFO=tan∠HDE=![]() =
=![]() .
.
点睛: 本题主要是考查切线的性质及解直角三角形的应用,关键是利用平行把已知角代换成其它相等的容易求出其正切值的角.


科目:初中数学 来源: 题型:
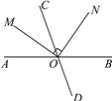
【题目】如图,直线AB,CD相交于点O,射线OM平分∠AOC,ON⊥OM.
(1)若∠BOD=70°,求∠AOM和∠CON的度数;
(2)若∠BON=50°,求∠AOM和∠CON的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在数轴上有三个点![]() .
.![]() .
.![]() ,完成系列问题:
,完成系列问题:
![]()
(1)将点![]() 向右移动六个单位长度到点
向右移动六个单位长度到点![]() ,在数轴上表示出点
,在数轴上表示出点![]() .
.
(2)在数轴上找到点![]() ,使点
,使点![]() 到
到![]() .
.![]() 两点的距离相等.并在数轴上标出点
两点的距离相等.并在数轴上标出点![]() 表示的数.
表示的数.
(3)在数轴上有一点![]() ,满足点
,满足点![]() 到点
到点![]() 与点
与点![]() 到点
到点![]() 的距离和是
的距离和是![]() ,则点
,则点![]() 表示的数是__________.
表示的数是__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:我们知道,分数可分为“真分数”和“假分数”,而假分数都可化为带分数,如![]() 我们定义:在分式中,对于只含有一个字母的分式,当分子的次数大于或等于分母的次数时,我们称之为“假分式”,当分子的次数小于分母的次数时,我们称之为“真分式”,如
我们定义:在分式中,对于只含有一个字母的分式,当分子的次数大于或等于分母的次数时,我们称之为“假分式”,当分子的次数小于分母的次数时,我们称之为“真分式”,如![]() 这样的分式就是假分式;再如:
这样的分式就是假分式;再如:![]() 这样的分式就是真分式。类似的,假分式也可以化为带分式(即:整式与真分式的和的形式),如:
这样的分式就是真分式。类似的,假分式也可以化为带分式(即:整式与真分式的和的形式),如:
![]()
请解决下列问题:
(1)分式![]() 是_____分式(填“真”或“假”);
是_____分式(填“真”或“假”);
(2)将假分式![]() 化为带分式;
化为带分式;
(3)若分式![]() 的值为整数,直接写出所有符合条件的正整数
的值为整数,直接写出所有符合条件的正整数![]() 的值。
的值。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现在,某商场进行促销活动,出售一种优惠购物卡(注:此卡只作为购物优惠凭证不能顶替货款),花300元买这种卡后,凭卡可在这家商场按标价的8折购物.
(1)顾客购买多少元金额的商品时,买卡与不买卡花钱相等?在什么情况下购物合算?
(2)小张要买一台标价为3500元的冰箱,如何购买合算?小张能节省多少元钱?
(3)小张按合算的方案,把这台冰箱买下,如果红旗商场还能盈利25%,这台冰箱的进价是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
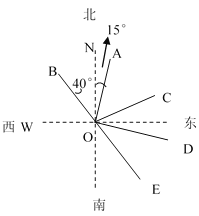
【题目】如图,射线OA的方向是北偏东15°,射线OB的方向是北偏西40°,∠AOB=∠AOC,射线OE是射线OB的反向延长线.
(1)求射线OC的方向角;
(2)求∠COE的度数;
(3)若射线OD平分∠COE,求∠AOD的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场销售一种西装和领带,西装每套定价200元,领带每条定价40元.国庆节期间商场决定开展促销活动,活动期间向客户提供两种优惠方案:
方案一:买一套西装送一条领带;
方案二:西装和领带都按定价的90%付款.
现某客户要到该商场购买西装20套,领带x(![]() ).
).
(1)若该客户按方案一购买,需付款多少元(用含x的式子表示)?若该客户按方案二购买,需付款多少元(用含x的式子表示)?
(2)若![]() ,通过计算说明此时按哪种方案购买较为合算;
,通过计算说明此时按哪种方案购买较为合算;
(3)当![]() 时,你能给出一种更为省钱的购买方法吗?试写出你的购买方法和所需费用.
时,你能给出一种更为省钱的购买方法吗?试写出你的购买方法和所需费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
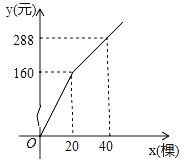
【题目】 为更新果树品种,某果园计划新购进A、B两个品种的果树苗栽植培育,若计划购进这两种果树苗共45棵,其中A种苗的单价为7元/棵,购买B种苗所需费用y(元)与购买数量x(棵)之间存在如图所示的函数关系.
(1)求y与x的函数关系式;
(2)若在购买计划中,B种苗的数量不超过35棵,但不少于A种苗的数量,请设计购买方案,使总费用最低,并求出最低费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】填空并完成以下证明: 已知,如图,∠1=∠ACB,∠2=∠3,FH⊥AB于H,求证:CD⊥AB.
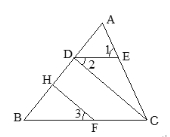
证明:∵∠1=∠ACB(已知)
∴DE∥BC( )
∴∠2= ( )
∵∠2=∠3(已知)
∴∠3= (等量代换)
∴CD∥FH( )
∴∠BDC=∠BHF( )
又∵FH⊥AB(已知)
∴
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com