
【题目】填空并完成以下证明: 已知,如图,∠1=∠ACB,∠2=∠3,FH⊥AB于H,求证:CD⊥AB.
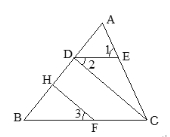
证明:∵∠1=∠ACB(已知)
∴DE∥BC( )
∴∠2= ( )
∵∠2=∠3(已知)
∴∠3= (等量代换)
∴CD∥FH( )
∴∠BDC=∠BHF( )
又∵FH⊥AB(已知)
∴
【答案】同位角相等,两直线平行; ∠DCB; 两直线平行,内错角相等; ∠DCB; 同位角相等,两直线平行; 两直线平行,同位角相等; CD⊥AB.
【解析】
先根据垂直的定义得出∠BHF=90°,再由∠1=∠ACB得出DE/IBC,故可得出∠2=∠BCD,根据∠2=∠3得出∠3=∠BCD,所以CD//FH,由平行线的性
质即可得出结论.
证明:∵∠1=∠ACB(已知)
∴DE∥BC( 同位角相等,两直线平行 )
∴∠2= ∠DCB ( 两直线平行,内错角相等 )
∵∠2=∠3(已知)
∴∠3= ∠DCB
∴CD∥FH( 同位角相等,两直线平行. )
∴∠BDC=∠BHF(两直线平行,同位角相等 )
又∵FH⊥AB(已知)
∴ CD⊥AB


 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案科目:初中数学 来源: 题型:
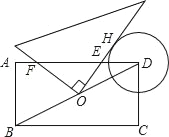
【题目】如图,在矩形ABCD中,AB=2,BC=4,⊙D的半径为1.现将一个直角三角板的直角顶点与矩形的对称中心O重合,绕着O点转动三角板,使它的一条直角边与⊙D切于点H,此时两直角边与AD交于E,F两点,则tan∠EFO的值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB∥CD , ∠BED=110°,BF平分∠ABE,DF平分∠CDE,则∠BFD= ( )
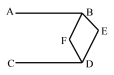
A.110°B.115°C.125°D.130°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图, 在四边形ABCD中,AD∥BC, E为CD的中点,连接 AE 、BE ,BE⊥AE, 延长AE交BC的延长线于 F,求证:(1) BE平分∠ABC (2)AB=BC+AD
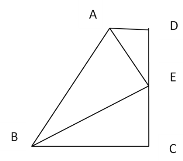
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)小河的同旁有甲、乙两个村庄(左图),现计划在河岸AB上建一个水泵站,向两村供水,用以解决村民生活用水问题。(保留作图痕迹)
①如果要求水泵站到甲、乙两村庄的距离相等,水泵站M应建在河岸AB上的何处?
②如果要求建造水泵站,供水管道使用建材最省,水泵站N又应建在河岸AB上的何处?

(2)如图,作出△ABC关于直线l的对称图形;
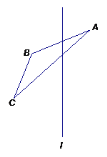
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现代互联网技术的广泛应用,催生了快递行业的高速发展,据调查,某家快递公司,今年三月份与五月份完成投递的快件总件数分别是5万件和![]() 万件,现假定该公司每月投递的快件总件数的增长率相同.
万件,现假定该公司每月投递的快件总件数的增长率相同.
![]() 求该公司投递快件总件数的月平均增长率;
求该公司投递快件总件数的月平均增长率;
![]() 如果平均每人每月可投递快递
如果平均每人每月可投递快递![]() 万件,那么该公司现有的16名快递投递员能否完成今年6月份的快递投递任务?
万件,那么该公司现有的16名快递投递员能否完成今年6月份的快递投递任务?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,AC=30cm,BC=40cm.点P从点A出发,以5cm/s的速度沿AC向终点C匀速移动.过点P作PQ⊥AB,垂足为点Q,以PQ为边作正方形PQMN,点M在AB边上,连接CN.设点P移动的时间为t(s).

(1)PQ=______;(用含t的代数式表示)
(2)当点N分别满足下列条件时,求出相应的t的值;①点C,N,M在同一条直线上;②点N落在BC边上;
(3)当△PCN为等腰三角形时,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】古巴比伦的记数法是六十进制的,用 ![]() 表示1,用
表示1,用 ![]() 表示10,这两种符号能表示一直到59的数字,例如,32可以用
表示10,这两种符号能表示一直到59的数字,例如,32可以用 ![]() 表示。从60起,开始使用符号组,从右往左依次是个位、六十位、三千六百位……(每一位的数值都是上一位的60倍),例如,
表示。从60起,开始使用符号组,从右往左依次是个位、六十位、三千六百位……(每一位的数值都是上一位的60倍),例如, ![]() 的个位表示23个1,六十位表示2个60,所以这个符号表示143。则下列表示3812的符号是( )
的个位表示23个1,六十位表示2个60,所以这个符号表示143。则下列表示3812的符号是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com