
【题目】如图,AB∥CD , ∠BED=110°,BF平分∠ABE,DF平分∠CDE,则∠BFD= ( )
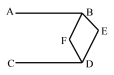
A.110°B.115°C.125°D.130°
【答案】C
【解析】
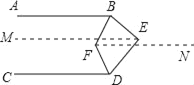
先过点E作EM∥AB,过点F作FN∥AB,由AB∥CD,即可得EM∥AB∥CD∥FN,然后根据两直线平行,同旁内角互补,由∠BED=110°,即可求得∠ABE+∠CDE=250°,又由BF平分∠ABE,DF平分∠CDE,根据角平分线的性质,即可求得∠ABF+∠CDF的度数,又由两直线平行,内错角相等,即可求得∠BFD的度数.
解:如图,过点E作EM∥AB,过点F作FN∥AB,
∵AB∥CD,
∴EM∥AB∥CD∥FN,
∴∠ABE+∠BEM=180°,∠CDE+∠DEM=180°,
∴∠ABE+∠BED+∠CDE=360°,
∵∠BED=110°,
∴∠ABE+∠CDE=250°
∵BF平分∠ABE,DF平分∠CDE,
∴∠ABF=![]() ∠ABE,∠CDF=
∠ABE,∠CDF=![]() ∠CDE,
∠CDE,
∴∠ABF+∠CDF=![]() (∠ABE+∠CDE)=125°,
(∠ABE+∠CDE)=125°,
∵∠DFN=∠CDF,∠BFN=∠ABF,
∴∠BFD=∠BFN+∠DFN=∠ABF+∠CDF=125°.
故选:C.


科目:初中数学 来源: 题型:
【题目】如图,在数轴上有三个点![]() .
.![]() .
.![]() ,完成系列问题:
,完成系列问题:
![]()
(1)将点![]() 向右移动六个单位长度到点
向右移动六个单位长度到点![]() ,在数轴上表示出点
,在数轴上表示出点![]() .
.
(2)在数轴上找到点![]() ,使点
,使点![]() 到
到![]() .
.![]() 两点的距离相等.并在数轴上标出点
两点的距离相等.并在数轴上标出点![]() 表示的数.
表示的数.
(3)在数轴上有一点![]() ,满足点
,满足点![]() 到点
到点![]() 与点
与点![]() 到点
到点![]() 的距离和是
的距离和是![]() ,则点
,则点![]() 表示的数是__________.
表示的数是__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场销售一种西装和领带,西装每套定价200元,领带每条定价40元.国庆节期间商场决定开展促销活动,活动期间向客户提供两种优惠方案:
方案一:买一套西装送一条领带;
方案二:西装和领带都按定价的90%付款.
现某客户要到该商场购买西装20套,领带x(![]() ).
).
(1)若该客户按方案一购买,需付款多少元(用含x的式子表示)?若该客户按方案二购买,需付款多少元(用含x的式子表示)?
(2)若![]() ,通过计算说明此时按哪种方案购买较为合算;
,通过计算说明此时按哪种方案购买较为合算;
(3)当![]() 时,你能给出一种更为省钱的购买方法吗?试写出你的购买方法和所需费用.
时,你能给出一种更为省钱的购买方法吗?试写出你的购买方法和所需费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
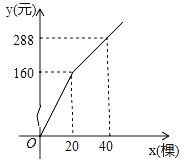
【题目】 为更新果树品种,某果园计划新购进A、B两个品种的果树苗栽植培育,若计划购进这两种果树苗共45棵,其中A种苗的单价为7元/棵,购买B种苗所需费用y(元)与购买数量x(棵)之间存在如图所示的函数关系.
(1)求y与x的函数关系式;
(2)若在购买计划中,B种苗的数量不超过35棵,但不少于A种苗的数量,请设计购买方案,使总费用最低,并求出最低费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地区2014年投入教育经费2900万元,2016年投入教育经费3509万元.
(1)求2014年至2016年该地区投入教育经费的年平均增长率;
(2)按照义务教育法规定,教育经费的投入不低于国民生产总值的百分之四,结合该地区国民生产总值的增长情况,该地区到2018年需投入教育经费4250万元,如果按(1)中教育经费投入的增长率,到2018年该地区投入的教育经费是否能达到4250万元?请说明理由.
(参考数据: ![]() =1.1,
=1.1, ![]() =1.2,
=1.2, ![]() =1.3,
=1.3, ![]() =1.4)
=1.4)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个寻宝游戏的寻宝通道如图①所示,通道由在同一平面内的AB,BC,CA,OA, OB,OC组成。为记录寻宝者的行进路线,在BC的中点M处放置了一台定位仪器,设寻宝者行进的时间为x,寻宝者与定位仪器之间的距离为y,若寻宝者匀速行进,且表示y与x的函数关系的图像大致如图②所示,则寻宝者的行进路线可能为:

A. A→O→B B. B→A→C C. B→O→C D. C→B→O
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=6,BC=4,过对角线BD中点O的直线分别交AB,CD边于点E,F.
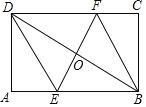
(1)求证:四边形BEDF是平行四边形;(2)当四边形BEDF是菱形时,求EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】填空并完成以下证明: 已知,如图,∠1=∠ACB,∠2=∠3,FH⊥AB于H,求证:CD⊥AB.
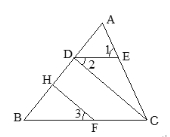
证明:∵∠1=∠ACB(已知)
∴DE∥BC( )
∴∠2= ( )
∵∠2=∠3(已知)
∴∠3= (等量代换)
∴CD∥FH( )
∴∠BDC=∠BHF( )
又∵FH⊥AB(已知)
∴
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,∠ABC=90°,D是BC的中点,E是AD的中点,过点A作AF∥BC交BE的延长线于点F.
(1)证明四边形ADCF是菱形;
(2)若AC=4,AB=5,求菱形ADCF的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com