
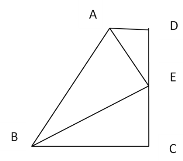
【题目】如图, 在四边形ABCD中,AD∥BC, E为CD的中点,连接 AE 、BE ,BE⊥AE, 延长AE交BC的延长线于 F,求证:(1) BE平分∠ABC (2)AB=BC+AD
【答案】(1)见解析;(2)见解析
【解析】
(1)根据AD//BC可知∠DAE=∠F ,∠D=∠ECF,再根据E是CD的中点可求出△ADE≌△FCE,根据全等三角形的性质可得AE=EF ,AD=CF,由BE⊥AE可得∠AEB=∠FEB可证△ABE≌△FBE即可解答.
(2)由(1)知 AD=CF, △ABE≌△FBE,可判断出AB= BF,由BF=BC+CF=BC+AD即可证.
证明: 如图 延长AE交BC的延长线于 F,
(1)∵ AD∥BC
∴ ∠DAE=∠F ∠D=∠ECF
∵ E为CD中点
∴ DE=CE
∵在△ADE和△FCE中
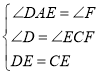
∴ △ADE≌△FCE (AAS)
∴ AE=EF,AD=CF
又∵ BE⊥AE
∴ ∠AEB=∠FEB=90°
∵在△ABE和△FBE中
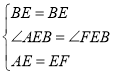
∴ △ABE≌△FBE (SAS)
∴∠ABE=∠FBE
则BE平分∠ABC
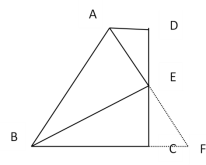
(2)由(1)知 AD=CF △ABE≌△FBE
∴AB=BF
∵BF=BC+CF
∴BF=BC+CF=BC+AD
∴AB=BC+AD


科目:初中数学 来源: 题型:
【题目】阅读下列材料:我们知道,分数可分为“真分数”和“假分数”,而假分数都可化为带分数,如![]() 我们定义:在分式中,对于只含有一个字母的分式,当分子的次数大于或等于分母的次数时,我们称之为“假分式”,当分子的次数小于分母的次数时,我们称之为“真分式”,如
我们定义:在分式中,对于只含有一个字母的分式,当分子的次数大于或等于分母的次数时,我们称之为“假分式”,当分子的次数小于分母的次数时,我们称之为“真分式”,如![]() 这样的分式就是假分式;再如:
这样的分式就是假分式;再如:![]() 这样的分式就是真分式。类似的,假分式也可以化为带分式(即:整式与真分式的和的形式),如:
这样的分式就是真分式。类似的,假分式也可以化为带分式(即:整式与真分式的和的形式),如:
![]()
请解决下列问题:
(1)分式![]() 是_____分式(填“真”或“假”);
是_____分式(填“真”或“假”);
(2)将假分式![]() 化为带分式;
化为带分式;
(3)若分式![]() 的值为整数,直接写出所有符合条件的正整数
的值为整数,直接写出所有符合条件的正整数![]() 的值。
的值。
查看答案和解析>>
科目:初中数学 来源: 题型:
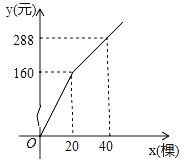
【题目】 为更新果树品种,某果园计划新购进A、B两个品种的果树苗栽植培育,若计划购进这两种果树苗共45棵,其中A种苗的单价为7元/棵,购买B种苗所需费用y(元)与购买数量x(棵)之间存在如图所示的函数关系.
(1)求y与x的函数关系式;
(2)若在购买计划中,B种苗的数量不超过35棵,但不少于A种苗的数量,请设计购买方案,使总费用最低,并求出最低费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个寻宝游戏的寻宝通道如图①所示,通道由在同一平面内的AB,BC,CA,OA, OB,OC组成。为记录寻宝者的行进路线,在BC的中点M处放置了一台定位仪器,设寻宝者行进的时间为x,寻宝者与定位仪器之间的距离为y,若寻宝者匀速行进,且表示y与x的函数关系的图像大致如图②所示,则寻宝者的行进路线可能为:

A. A→O→B B. B→A→C C. B→O→C D. C→B→O
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=6,BC=4,过对角线BD中点O的直线分别交AB,CD边于点E,F.
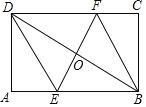
(1)求证:四边形BEDF是平行四边形;(2)当四边形BEDF是菱形时,求EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】达川区花椒产业扶贫初见成效,农户张三今年花椒产业喜获丰收,一天他带了若干花椒进城出售,为了方便,他带了一些零钱备用.按市场售出一些后,又降价出售.售出花椒斤数x与他手中持有的钱数y(含备用零钱)的关系如图所示,结合图像回答下列问题:
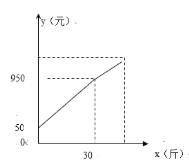
(1)张三自带的零钱是多少?
(2)降价前他每斤花椒出售的价格是多少?
(3)降价后他按每斤25元将剩余的花椒售完,这时他手中的钱(含备用的钱)是1150元,问他一共带了多少斤花椒?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】填空并完成以下证明: 已知,如图,∠1=∠ACB,∠2=∠3,FH⊥AB于H,求证:CD⊥AB.
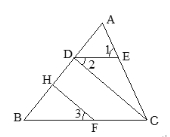
证明:∵∠1=∠ACB(已知)
∴DE∥BC( )
∴∠2= ( )
∵∠2=∠3(已知)
∴∠3= (等量代换)
∴CD∥FH( )
∴∠BDC=∠BHF( )
又∵FH⊥AB(已知)
∴
查看答案和解析>>
科目:初中数学 来源: 题型:
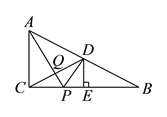
【题目】如图,在![]() 中,
中, ![]() ,点
,点![]() 是
是![]() 边的中点,过
边的中点,过![]() 作
作![]() 于点
于点![]() ,点
,点![]() 是边
是边![]() 上的一个动点,
上的一个动点, ![]() 与
与![]() 相交于点
相交于点![]() .当
.当![]() 的值最小时,
的值最小时, ![]() 与
与![]() 之间的数量关系是__________.
之间的数量关系是__________.
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com