【题目】古巴比伦的记数法是六十进制的，用 
表示1，用 
表示10，这两种符号能表示一直到59的数字，例如，32可以用 
表示。从60起，开始使用符号组，从右往左依次是个位、六十位、三千六百位……(每一位的数值都是上一位的60倍)，例如， 
的个位表示23个1，六十位表示2个60，所以这个符号表示143。则下列表示3812的符号是( )
A.
B.
C.
D.
科目：初中数学 来源： 题型：
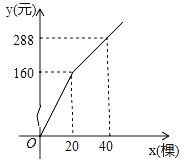
【题目】 为更新果树品种，某果园计划新购进A、B两个品种的果树苗栽植培育，若计划购进这两种果树苗共45棵，其中A种苗的单价为7元/棵，购买B种苗所需费用y（元）与购买数量x（棵）之间存在如图所示的函数关系．
（1）求y与x的函数关系式；
（2）若在购买计划中，B种苗的数量不超过35棵，但不少于A种苗的数量，请设计购买方案，使总费用最低，并求出最低费用．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】填空并完成以下证明： 已知，如图，∠1＝∠ACB，∠2＝∠3，FH⊥AB于H，求证：CD⊥AB．
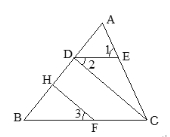
证明：∵∠1＝∠ACB（已知）
∴DE∥BC（ ）
∴∠2＝ （ ）
∵∠2＝∠3（已知）
∴∠3＝ （等量代换）
∴CD∥FH（ ）
∴∠BDC＝∠BHF（ ）
又∵FH⊥AB（已知）
∴
查看答案和解析>>
科目：初中数学 来源： 题型：
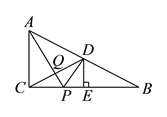
【题目】如图，在
中， 
，点
是
边的中点，过
作
于点
，点
是边
上的一个动点， 
与
相交于点
．当
的值最小时， 
与
之间的数量关系是__________．
A. 
B. 
C. 
D. 
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在正方形ABCD中，点E、F在对角线BD上，且BF＝DE．
⑴求证：四边形AECF是菱形．
⑵若AB＝2，BF＝1，求四边形AECF的面积．
查看答案和解析>>
科目：初中数学 来源： 题型：
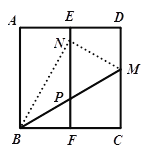
【题目】如图，在正方形纸片ABCD中，E，F分别是AD，BC的中点，沿过点B的直线折叠，使点C落在EF上，落点为N，折痕交CD边于点M，BM与EF交于点P，再展开．则下列结论中：①CM＝DM；②∠ABN＝30°；③AB2＝3CM2；④△PMN是等边三角形．
正确的有（ ）
A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在Rt△ABC中，∠ABC=90°，D是BC的中点，E是AD的中点，过点A作AF∥BC交BE的延长线于点F．
（1）证明四边形ADCF是菱形；
（2）若AC=4，AB=5，求菱形ADCF的面积．
查看答案和解析>>
科目：初中数学 来源： 题型：
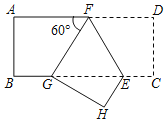
【题目】如图，点E、F分别在矩形ABCD的边BC、AD上，把这个矩形沿EF折叠后，点D恰好落在BC边上的G点处，且∠AFG=60°
（1）求证：GE=2EC；
（2）连接CH、DG，试证明：CH∥DG．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
