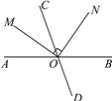
[题目]如图.直线AB.CD相交于点O.射线OM平分∠AOC.ON⊥OM.(1)若∠BOD＝70°.求∠AOM和∠CON的度数,(2)若∠BON＝50°.求∠AOM和∠CON的度数．题目和参考答案——青夏教育精英家教网—

精英家教网 > 初中数学 > 题目详情

【题目】如图，直线AB，CD相交于点O，射线OM平分∠AOC，ON⊥OM.

(1)若∠BOD＝70°，求∠AOM和∠CON的度数；

(2)若∠BON＝50°，求∠AOM和∠CON的度数．

【答案】（1）55°（2）50°

【解析】

（1）直接利用垂线的定义结合角平分线的定义得出答案．
（2）利用垂线的定义结合角平分线的定义得出答案．

(1)因为∠BOD＝70°，所以∠AOC＝70°.

因为射线OM平分∠AOC，所以∠AOM＝∠MOC＝35°.因为ON⊥OM，所以∠CON＝90°－35°＝55°.

(2)因为ON⊥OM，∠BON＝50°，

所以∠AOM＝180°－90°－50°＝40°.

因为射线OM平分∠AOC，所以∠AOM＝∠MOC＝40°，

所以∠CON＝90°－40°＝50°.

练习册系列答案

新课标同步训练系列答案

一线名师口算应用题天天练一本全系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：

【题目】如图，抛物线y=ax2+bx+c（a≠0）与x轴、y轴分别交于A（﹣1，0）、B（3，0）、C（0，3）三点．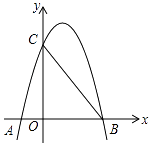

（1）试求抛物线的解析式；
（2）P是直线BC上方抛物线上的一个动点，设P的横坐标为t，P到BC的距离为h，求h与t的函数关系式，并求出h的最大值．
（3）设点M是x轴上的动点，在平面直角坐标系中，是否存在点N，使得以点A、C、M、N为顶点的四边形是菱形？若存在，求出所有符合条件的点N坐标；若不存在，说明理由．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】在△ABC中，AB=AC=6，cos∠B= ，以点B为圆心，AB为半径作圆B，以点C为圆心，半径长为13作圆C，圆B与圆C的位置关系是（）
A.外切
B.相交
C.内切
D.内含

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】解不等式组将其解集在数轴上表示出来，并写出这个不等式组的整数解．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】文山州某中学为普遍提高学生身体素质，开展每天“阳光体育一小时”活动，根据实际情况决定开设A、篮球；B、乒乓球；C、羽毛球；D、足球四种运动项目，为了解学生最喜欢哪一种运动项目，随机抽取了一部分学生进行调查，每名学生必须且只能选择最喜爱的一项运动项目，并将调查结果制作成如下两幅不完整的统计图，请结合图中的信息解答下列问题：

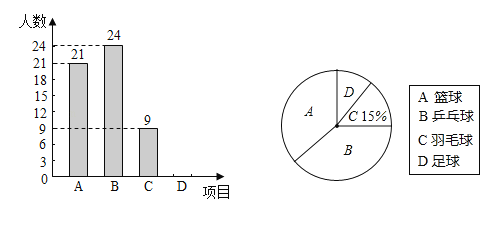
（1）这次被抽查的学生有人；请补全条形统计图；

（2）在统计图中，“乒乓球”对应扇形的圆心角是度；

（3）若该中学共有3600名学生，喜欢篮球的学生约有多少人？

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】如图，将长方形ABCD沿着对角线BD折叠，使点C落在处，交AD于点E．

（1）试判断△BDE的形状，并说明理由；

（2）若，，求△BDE的面积．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】甲、乙两车从A地出发，沿同一路线驶向B地. 甲车先出发匀速驶向B地，40 min后，乙车出发，匀速行驶一段时间后，在途中的货站装货耗时半小时. 由于满载货物，为了行驶安全，速度减少了50 km/h，结果与甲车同时到达B地. 甲乙两车距A地的路程y（km）与乙车行驶时间x（h）之间的函数图象如图所示，则下列说法：①a＝4.5；②甲的速度是60 km/h；③乙出发80 min追上甲；④乙刚到达货站时，甲距B地180 km.其中正确的有（）