
【题目】在△ABC中,AB=AC=6,cos∠B= ![]() ,以点B为圆心,AB为半径作圆B,以点C为圆心,半径长为13作圆C,圆B与圆C的位置关系是( )
,以点B为圆心,AB为半径作圆B,以点C为圆心,半径长为13作圆C,圆B与圆C的位置关系是( )
A.外切
B.相交
C.内切
D.内含
科目:初中数学 来源: 题型:
【题目】已知线段AB,用尺规作∠ABC=90°,作法如下:
小明的作法:(1)分别以A、B为圆心AB长为半径画弧,两弧交于点P;(2)以P为圆心,AB长为半径画弧交AP的延长线于C;连接AC,则∠ABC=90° |
|
(1)请证明∠ABC=90°;
(2)请你用不同的方法,用尺规作∠ABC=90°.
(要求:保留作图痕迹,不写作法,并用2B铅笔把作图痕迹描粗)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明在海湾森林公园放风筝.如图所示,小明在A处,风筝飞到C处,此时线长BC为40米,若小明双手牵住绳子的底端B距离地面1.5米,从B处测得C处的仰角为60°,求此时风筝离地面的高度CE.(计算结果精确到0.1米, ![]() ≈1.732)
≈1.732)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是某年的日历表,在此日历表上可以用一个矩形圈出3×3个位置的9个数(如3,4,5,10,11,12,17,18,19).若用这样的矩形圈圈这张日历表的9个数,则圈出的9个数的和不可能为下列数中的( )

A. 81 B. 90 C. 108 D. 216
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,已知正比例函数的图象与反比例函数y= ![]() 的图象交于点A(m,4).
的图象交于点A(m,4).
(1)求正比例函数的解析式;
(2)将正比例函数的图象向下平移6个单位得到直线l,设直线l与x轴的交点为B,求∠ABO的正弦值.
查看答案和解析>>
科目:初中数学 来源: 题型:
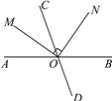
【题目】如图,直线AB,CD相交于点O,射线OM平分∠AOC,ON⊥OM.
(1)若∠BOD=70°,求∠AOM和∠CON的度数;
(2)若∠BON=50°,求∠AOM和∠CON的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,AE是△ABC的角平分线;ED平分∠AEB交AB于点D;∠CAE=∠B.
(1)如果AC=3.5 cm,求AB的长度;
(2)猜想:ED与AB的位置关系,并证明你的猜想。

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com