
【题目】在平面直角坐标系xOy中,已知正比例函数的图象与反比例函数y= ![]() 的图象交于点A(m,4).
的图象交于点A(m,4).
(1)求正比例函数的解析式;
(2)将正比例函数的图象向下平移6个单位得到直线l,设直线l与x轴的交点为B,求∠ABO的正弦值.
【答案】
(1)解:∵反比例函数y= ![]() 的图象经过A(m,4),
的图象经过A(m,4),
∴4= ![]() ,解得m=2.
,解得m=2.
∴点A的坐标为(2,4).
设正比例函数的解析式为y=kx,
∵正比例函数的图象经过点A(2,4),
∴可得 4=2k,解得k=2.
∴正比例函数的解析式是y=2x
(2)解:∵正比例函数向下平移6个单位得到直线l,
∴直线l的表达式为y=2x﹣6
∵直l与x轴的交点为B,
∴点B的坐标是(3,0)
∴由勾股定理可知:AB= ![]() .
.
∴sin∠ABO= ![]() =
= ![]()
【解析】(1)由于点A经过(m,4)所以可求出m=2,再将A(2,4)代入反比例函数中即可求出k的值.(2)先求平移后的直线l的解析式,然后求出B的坐标,利用勾股定理可求出AB的长度,利用正弦的定义即可求出∠ABO的正弦值.
【考点精析】关于本题考查的解直角三角形,需要了解解直角三角形的依据:①边的关系a2+b2=c2;②角的关系:A+B=90°;③边角关系:三角函数的定义.(注意:尽量避免使用中间数据和除法)才能得出正确答案.


科目:初中数学 来源: 题型:
【题目】小明骑车从家出发,先向东骑行1km到达A村,继续向东骑行4km到达B村,然后向西骑行8km到达C村,最后回到家.
(1) 以快递公司为原点,以向东方向为正方向,用1 cm表示1 km,画出数轴,并在数轴上表示出A、B、C三个店的位置;
(2) C店离A店有多远?
(3) 快递员一共骑行了多少千米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】骑自行车旅行越来越受到人们的喜爱,各种品牌的山地自行车相继投放市场,某车行经营的A型车去年3月份销售总额为3.2万元,今年经过改造升级后A型车每辆销售价比去年增加400元,若今年3月份与去年3月份卖出的A型车数量相同,则今年3月份A型车销售总额将比去年3月份销售总额增加25%.
(1)求今年3月份A型车每辆销售价多少元?
(2)该车行计划今年4月份新进一批A型车和B型车共50辆,且B型车的进货数量不超过A型车数量的两倍,A、B两种型号车的进货和销售价格如下表,问应如何进货才能使这批车获利最多?
A型车 | B型车 | |
进货价格(元/辆) | 1100 | 1400 |
销售价格(元/辆) | 今年的销售价格 | 2400 |
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图A在数轴上所对应的数为﹣2.
(1)点B在点A右边距A点4个单位长度,求点B所对应的数;
(2)在(1)的条件下,点A以每秒2个单位长度沿数轴向左运动,点 B 以每秒2个单位长度沿数轴向右运动,当点A运动到﹣6所在的点处时,求A,B两点间距离.
(3)在(2)的条件下,现A点静止不动,B点再以每秒2个单位长度沿数轴向左运动时,经过多长时间A,B两点相距4个单位长度.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=AC=6,cos∠B= ![]() ,以点B为圆心,AB为半径作圆B,以点C为圆心,半径长为13作圆C,圆B与圆C的位置关系是( )
,以点B为圆心,AB为半径作圆B,以点C为圆心,半径长为13作圆C,圆B与圆C的位置关系是( )
A.外切
B.相交
C.内切
D.内含
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,二次函数y=x2﹣2x+m(m>0)的对称轴与比例系数为5的反比例函数图象交于点A,与x轴交于点B,抛物线的图象与y轴交于点C,且OC=3OB.
(1)求点A的坐标;
(2)求直线AC的表达式;
(3)点E是直线AC上一动点,点F在x轴上方的平面内,且使以A、B、E、F为顶点的四边形是菱形,直接写出点F的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将长方形ABCD沿着对角线BD折叠,使点C落在![]() 处,
处,![]() 交AD于点E.
交AD于点E.
(1)试判断△BDE的形状,并说明理由;
(2)若![]() ,
,![]() ,求△BDE的面积.
,求△BDE的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,轮船在A处观测灯塔C位于北偏西70°方向上,轮船从A处以每小时20海里的速度沿南偏西50°方向匀速航行,1小时后到达码头B处,此时,观测灯塔C位于北偏西25°方向上,则灯塔C与码头B的距离是( )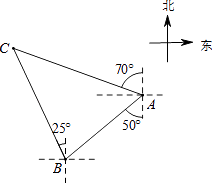
A.10 ![]() 海里
海里
B.10 ![]() 海里
海里
C.10 ![]() 海里
海里
D.20 ![]() 海里
海里
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com