
【题目】如图,在平面直角坐标系xOy中,二次函数y=x2﹣2x+m(m>0)的对称轴与比例系数为5的反比例函数图象交于点A,与x轴交于点B,抛物线的图象与y轴交于点C,且OC=3OB.
(1)求点A的坐标;
(2)求直线AC的表达式;
(3)点E是直线AC上一动点,点F在x轴上方的平面内,且使以A、B、E、F为顶点的四边形是菱形,直接写出点F的坐标.
【答案】
(1)
解:由题意可知二次函数图象的对称轴是直线x=1,反比例函数解析式是y= ![]() ,
,
把x=1代入y= ![]() ,得y=5,
,得y=5,
∴点A的坐标为(1,5);
(2)
解:由题意可得点B的坐标为(1,0),
∵OC=3OB,
∴OC=3,
∵m>0,
∴m=3,
可设直线AC的表达式是y=kx+3,
∵点A在直线AC上,
∴k=2,
∴直线AC的表达式是y=2x+3;
(3)
解:当AB、BE为菱形的边时,如图1,
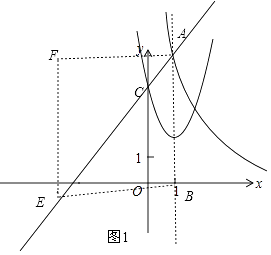
设E(x,2x+3),则BE= ![]() ,
,
∵四边形ABEF为菱形,
∴AB=BE=5,
∴ ![]() =5,解得x=1(E、A重合,舍去)或x=﹣3,
=5,解得x=1(E、A重合,舍去)或x=﹣3,
此时E(﹣3,﹣3),
∵EF∥AB且EF=AB,
∴F(﹣3,2),
当AB、AE为边时,则AE=AB=5,
同理可求得AE= ![]() ,
,
∴ ![]() =5,解得x=1﹣
=5,解得x=1﹣ ![]() (此时F点在第三象限,舍去)或x=1+
(此时F点在第三象限,舍去)或x=1+ ![]() ,
,
∴E(1+ ![]() ,5+2
,5+2 ![]() ),
),
∵EF∥AB且EF=AB,
∴F(1+ ![]() ,2
,2 ![]() );
);
当AB为对角线时,如图2,
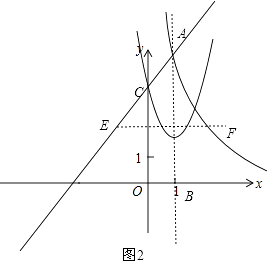
则EF过AB的中点,
∵A(1,5),B(1,0),
∴AB的中点为(1, ![]() ),
),
∵EF⊥AB,
∴EF∥x轴,
∴E点纵坐标为 ![]() ,代入y=2x+3可得
,代入y=2x+3可得 ![]() =2x+3,解得x=﹣
=2x+3,解得x=﹣ ![]() ,
,
∴E(﹣ ![]() ,
, ![]() ),
),
∴F( ![]() ,
, ![]() );
);
综上可知F点的坐标为(﹣3,2)或(1+ ![]() ,2
,2 ![]() )或(
)或( ![]() ,
, ![]() )
)
【解析】(1)可求得抛物线对称轴方程和反比例函数解析式,则可求得A点坐标;(2)可求得B点坐标,再由OC=3OB可求得C点坐标,利用待定系数法可求得直线AC的表达式;(3)当AB为菱形的边时,则BE=AB或AE=AB,设出E点坐标,可表示出BE的长,可得到关于E点坐标的方程,可求得E点坐标,由AB∥EF,则可求得F点的坐标;当AB为对角线时,则EF被AB垂直平分,则可求得E的纵坐标,从而可求得E点坐标,利用对称性可求得F点的坐标.


科目:初中数学 来源: 题型:
【题目】2016年11月3日,我国第一枚大型运载火箭“长征5号”在海南文昌航天发射场顺利升空,这标志着我国从航天大国迈向航天强国.如图,火箭从地面L处发射,当火箭到达A点时,从位于地面R处雷达站测得AR的距离是6km,仰角为42.4°;1秒后火箭到达B点,此时测得仰角为45.5°.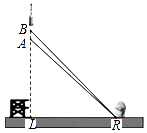
(1)求发射台与雷达站之间的距离LR;
(2)求这枚火箭从A到B的平均速度是多少?(结果精确到0.01,参考数据:sin42.4°≈0.67,cos42.4°≈0.74,tan42.4°≈0.905,sin45.5°≈0.71,cos45.5°≈0.70,tan45.5°≈1.02 )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下表记录的是今年长江某一周内的水位变化情况,这一周的上周末的水位已达到警戒水位![]() 米(正号表示水位比前一天上升,负号表示水位比前一天下降).
米(正号表示水位比前一天上升,负号表示水位比前一天下降).
星期 | 一 | 二 | 三 | 四 | 五 | 六 |
水位 变化(米) | +0.2 |
| -0.4 |
| +0.3 |
|
(1)本周哪一天长江的水位最高?位于警戒水位之上还是之下?
(2)与上周周末相比,本周周末长江的水位是上升了还是下降了?并通过计算说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,已知正比例函数的图象与反比例函数y= ![]() 的图象交于点A(m,4).
的图象交于点A(m,4).
(1)求正比例函数的解析式;
(2)将正比例函数的图象向下平移6个单位得到直线l,设直线l与x轴的交点为B,求∠ABO的正弦值.
查看答案和解析>>
科目:初中数学 来源: 题型:
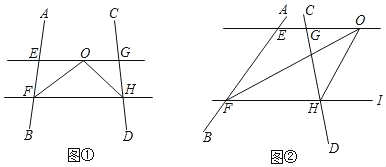
【题目】(探究)如图①,∠AFH和∠CHF的平分线交于点O,EG经过点O且平行于FH,分别与AB、CD交于点E、G.
(1)若∠AFH=60°,∠CHF=50°,则∠EOF=_____度,∠FOH=_____度.
(2)若∠AFH+∠CHF=100°,求∠FOH的度数.
(拓展)如图②,∠AFH和∠CHI的平分线交于点O,EG经过点O且平行于FH,分别与AB、CD交于点E、G.若∠AFH+∠CHF=α,直接写出∠FOH的度数.(用含a的代数式表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在梯形ABCD中,AD∥BC,∠ABC=90°,AB=4,AD=8,sin∠BCD= ![]() ,CE平分∠BCD,交边AD于点E,联结BE并延长,交CD的延长线于点P.
,CE平分∠BCD,交边AD于点E,联结BE并延长,交CD的延长线于点P. 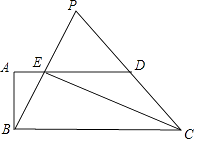
(1)求梯形ABCD的周长;
(2)求PE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,抛物线y=﹣x2+bx+c经过点A(3,0)和点B(2,3),过点A的直线与y轴的负半轴相交于点C,且tan∠CAO= ![]() .
. 
(1)求这条抛物线的表达式及对称轴;
(2)联结AB、BC,求∠ABC的正切值;
(3)若点D在x轴下方的对称轴上,当S△DBC=S△ADC时,求点D的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,BE平分∠ABC交AC边于点E,
(1)如图1,过点E作DE∥BC交AB于点D,求证:△BDE为等腰三角形;
(2)如图2,延长BE到D,∠ADB =∠ABC, AF⊥BD于F,AD=2,BF=3,求DF的长
(3)如图3,若AB=AC,AF⊥BD,∠ACD=![]() ∠ABC,判断BF、CD、DF的数量关系,并说明理由.
∠ABC,判断BF、CD、DF的数量关系,并说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com