
【题目】如图,在平面直角坐标系xOy中,抛物线y=﹣x2+bx+c经过点A(3,0)和点B(2,3),过点A的直线与y轴的负半轴相交于点C,且tan∠CAO= ![]() .
. 
(1)求这条抛物线的表达式及对称轴;
(2)联结AB、BC,求∠ABC的正切值;
(3)若点D在x轴下方的对称轴上,当S△DBC=S△ADC时,求点D的坐标.
【答案】
(1)解:把A(3,0)和点B(2,3)代入y=﹣x2+bx+c得到 ![]() ,
,
解得 ![]() ,
,
∴抛物线的解析式为y=﹣x2+2x+3,
对称轴x=1
(2)解:如图,作BE⊥OA于E.
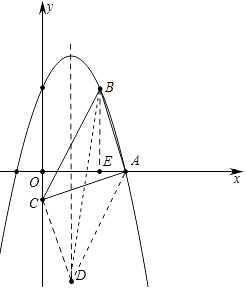
∵A(3,0),B(2,3),tan∠CAO= ![]() ,
,
∴OC=1,
∴BE=OA=3,AE=OC=1,∵AEB=∠AOC,
∴△AOC≌△BEA,
∴AC=AB,∠CAO=∠BAE,
∵∠ABE+∠BAE=90°,
∴∠CAO+∠BAE=90°,
∴∠CAB=90°,
∴△ABC是等腰直角三角形,
∴∠ABC=45°,
∴tan∠ABC=1
(3)解:如图过点C作CD∥AB交对称轴于D,

则S△DBC=S△ADC,
∵AB⊥AC,AB∥CD,
∴AC⊥CD,
∵直线AC的解析式为y= ![]() x﹣1,
x﹣1,
∴直线CD的解析式为y=﹣3x﹣1,当x=1时,y=﹣4,
∴点D的坐标为(1,﹣4).
【解析】(1)把A(3,0)和点B(2,3)代入y=﹣x2+bx+c,解方程组即可解决问题.(2)如图,作BE⊥OA于E.只要证明△AOC≌△BEA,推出△ABC是等腰直角三角形,即可解决问题.(3)如图过点C作CD∥AB交对称轴于D,则S△DBC=S△ADC , 先求出直线AC的解析式,再求出直线CD的解析式即可解决问题.
【考点精析】通过灵活运用抛物线与坐标轴的交点和解直角三角形,掌握一元二次方程的解是其对应的二次函数的图像与x轴的交点坐标.因此一元二次方程中的b2-4ac,在二次函数中表示图像与x轴是否有交点.当b2-4ac>0时,图像与x轴有两个交点;当b2-4ac=0时,图像与x轴有一个交点;当b2-4ac<0时,图像与x轴没有交点.;解直角三角形的依据:①边的关系a2+b2=c2;②角的关系:A+B=90°;③边角关系:三角函数的定义.(注意:尽量避免使用中间数据和除法)即可以解答此题.


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,△OAB的顶点A在x轴的正半轴上,BC=2AC , 点B、C在反比例函数y= ![]() (x>0)的图象上,则△OAB的面积为.
(x>0)的图象上,则△OAB的面积为.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,二次函数y=x2﹣2x+m(m>0)的对称轴与比例系数为5的反比例函数图象交于点A,与x轴交于点B,抛物线的图象与y轴交于点C,且OC=3OB.
(1)求点A的坐标;
(2)求直线AC的表达式;
(3)点E是直线AC上一动点,点F在x轴上方的平面内,且使以A、B、E、F为顶点的四边形是菱形,直接写出点F的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下面算式,解答问题:
![]()
![]()
![]() ……
……
(1)请求出1 3 5 7 9 11的结果为 ;
请求出1 3 5 7 9 29 的结果为 ;
(2)若n 表示正整数,请用含 n 的代数式表示1 3 5 7 9 (2n 1) (2n 1) 的值为
(3)请用上述规律计算: 41 43 45 77 79 的值(要求写出详细解答过程).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将长方形ABCD沿着对角线BD折叠,使点C落在![]() 处,
处,![]() 交AD于点E.
交AD于点E.
(1)试判断△BDE的形状,并说明理由;
(2)若![]() ,
,![]() ,求△BDE的面积.
,求△BDE的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把一张矩形纸片ABCD沿EF折叠后,点A落在CD边上的点A′处,点B落在点B′处,若∠2=40°,则图中∠1的度数为( ) 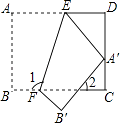
A.115°
B.120°
C.130°
D.140°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了了解某学校初四年级学生每周平均课外阅读时间的情况,随机抽查了该学校初四年级m名同学,对其每周平均课外阅读时间进行统计,绘制了如下条形统计图(图一)和扇形统计图(图二):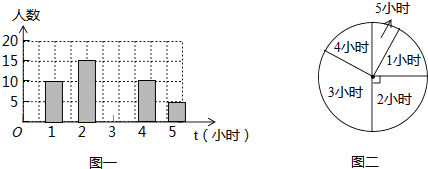
(1)根据以上信息回答下列问题:
①求m值.
②求扇形统计图中阅读时间为5小时的扇形圆心角的度数.
③补全条形统计图.
(2)直接写出这组数据的众数、中位数,求出这组数据的平均数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB、CD为 ![]() O的直径,弦AE//CD,连接BE交CD于点F,过点E作直线EP与CD的延长线交于点P,使
O的直径,弦AE//CD,连接BE交CD于点F,过点E作直线EP与CD的延长线交于点P,使 ![]() PED=
PED= ![]() C.
C.
(1)求证:PE是 ![]() O的切线;
O的切线;
(2)求证:ED平分 ![]() BEP;
BEP;
(3)若 ![]() O的半径为5,CF=2EF,求PD的长.
O的半径为5,CF=2EF,求PD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
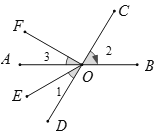
【题目】如图,直线 AB,CD 相交于点O,OE 平分∠AOD,OF⊥OC.
(1)图中∠AOF 的余角是_____ _____(把符合条件的角都填出来);
(2)如果∠AOC=120°,那么根据____ ______,可得∠BOD=__________°;
(3)如果∠1=32°,求∠2和∠3的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com