
【题目】如图,△ABC中,BE平分∠ABC交AC边于点E,
(1)如图1,过点E作DE∥BC交AB于点D,求证:△BDE为等腰三角形;
(2)如图2,延长BE到D,∠ADB =∠ABC, AF⊥BD于F,AD=2,BF=3,求DF的长
(3)如图3,若AB=AC,AF⊥BD,∠ACD=![]() ∠ABC,判断BF、CD、DF的数量关系,并说明理由.
∠ABC,判断BF、CD、DF的数量关系,并说明理由.

【答案】(1)证明见解析;(2)DF=1; (3)BF=CD+DF,理由见解析.
【解析】
(1)由角平分线和平行线的性质可得到∠BDE=∠DEB,可证得结论;
(2)作AH=AD,可得AH=BH=AD=2,从而HF= 1,在△AHD中,AH=AD,AF⊥HD,
得HF=FD=1;
(3)延长CD到M,使得CM=BD,连接AM,过点A作AN⊥CM于点N,则△ABD≌△ACM,根据全等三角形的性质可得出AD=AM,∠ADB=∠AMC,利用全等三角形的判定定理AAS可证出△ADF≌△ADN,根据全等三角形的性质可得出DF=DN=MN,再结合BD=CM即可找出BF=CD+DF.
(1)证明:
∵BE平分∠ABC,
∴∠ABE=∠EBC,
∵DE∥BC,
∴∠DEB=∠EBC=∠ABE,
∴BD=ED,
∴△DBE为等腰三角形;
(2)作AH=AD,

∴∠AHD=∠D,
∴∠1=![]() ∠AHD,
∠AHD,
∵∠AHD=∠1+∠3,
∴AH=BH=AD=2,
∴HF=BF-BH=3-2=1,
∵在△AHD中,AH=AD,AF⊥HD,
∴HF=FD=![]() HD,
HD,
∴DF=HF=1;
(3)解:在图中,延长CD到M,使得CM=BD,连接AM,过点A作AN⊥CM于点N,

∵BE平分∠ABC,∠ACD=![]() ∠ABC,
∠ABC,
∴∠ACM=∠ABD.
在△ABD和△ACM中,
 ,
,
∴△ABD≌△ACM(SAS),
∴AD=AM,∠ADB=∠AMC,
∴∠AMD=∠ADM,
∴∠ADF=ADN.
∵AN⊥DM,
∴DN=MN.
在△ADF和△ADN中,
 ,
,
∴△ADF≌△ADN(AAS),
∴DF=DN=MN.
∵BD=CM,
∴BF=BC-DF=CM-MN=CN=CD+DN=CD+DF.
即BF=CD+DF.


 导学教程高中新课标系列答案
导学教程高中新课标系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,二次函数y=x2﹣2x+m(m>0)的对称轴与比例系数为5的反比例函数图象交于点A,与x轴交于点B,抛物线的图象与y轴交于点C,且OC=3OB.
(1)求点A的坐标;
(2)求直线AC的表达式;
(3)点E是直线AC上一动点,点F在x轴上方的平面内,且使以A、B、E、F为顶点的四边形是菱形,直接写出点F的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了了解某学校初四年级学生每周平均课外阅读时间的情况,随机抽查了该学校初四年级m名同学,对其每周平均课外阅读时间进行统计,绘制了如下条形统计图(图一)和扇形统计图(图二):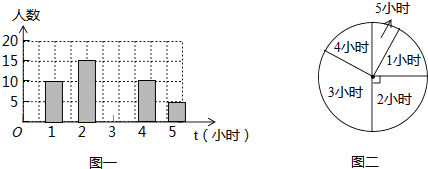
(1)根据以上信息回答下列问题:
①求m值.
②求扇形统计图中阅读时间为5小时的扇形圆心角的度数.
③补全条形统计图.
(2)直接写出这组数据的众数、中位数,求出这组数据的平均数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB、CD为 ![]() O的直径,弦AE//CD,连接BE交CD于点F,过点E作直线EP与CD的延长线交于点P,使
O的直径,弦AE//CD,连接BE交CD于点F,过点E作直线EP与CD的延长线交于点P,使 ![]() PED=
PED= ![]() C.
C.
(1)求证:PE是 ![]() O的切线;
O的切线;
(2)求证:ED平分 ![]() BEP;
BEP;
(3)若 ![]() O的半径为5,CF=2EF,求PD的长.
O的半径为5,CF=2EF,求PD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,轮船在A处观测灯塔C位于北偏西70°方向上,轮船从A处以每小时20海里的速度沿南偏西50°方向匀速航行,1小时后到达码头B处,此时,观测灯塔C位于北偏西25°方向上,则灯塔C与码头B的距离是( )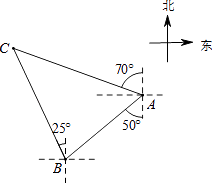
A.10 ![]() 海里
海里
B.10 ![]() 海里
海里
C.10 ![]() 海里
海里
D.20 ![]() 海里
海里
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我省某工艺厂为全运会设计了一款成本为每件20元的工艺品,投放市场试销后发现每天的销售量y(件)是售价x(元/件)的一次函数。当售价为22元/件时,每天销售量为780件;当售价为25元/件时,每天销售量为750件。
(1)求y与x的函数关系式;
(2)如果该工艺品售价最高不超过每件30元,那么售价定为每件多少元时,工艺厂销售该工艺品每天获得的利润最大?最大利润是多少元?(利润=售价-成本)
查看答案和解析>>
科目:初中数学 来源: 题型:
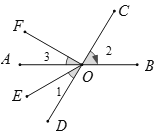
【题目】如图,直线 AB,CD 相交于点O,OE 平分∠AOD,OF⊥OC.
(1)图中∠AOF 的余角是_____ _____(把符合条件的角都填出来);
(2)如果∠AOC=120°,那么根据____ ______,可得∠BOD=__________°;
(3)如果∠1=32°,求∠2和∠3的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市某商场有甲、乙两种商品,甲种每件进价15元,售价20元;乙种每件进价35元,售价45元.
(1)若商家同时购进甲、乙两种商品100件,设甲商品购进x件,售完此两种商品总利润为y 元.写出y与x的函数关系式.
(2)该商家计划最多投入3000元用于购进此两种商品共100件,则至少要购进多少件甲种商品?若售完这些商品,商家可获得的最大利润是多少元?
(3)“五一”期间,商家对甲、乙两种商品进行表中的优惠活动,小王到该商场一次性付款324元购买此类商品,商家可获得的最小利润和最大利润各是多少?
打折前一次性购物总金额 | 优惠措施 |
不超过400元 | 售价打九折 |
超过400元 | 售价打八折 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com