
����Ŀ����̽������ͼ�٣���AFH�͡�CHF��ƽ���߽��ڵ�O��EG������O��ƽ����FH���ֱ���AB��CD���ڵ�E��G��
(1)����AFH��60������CHF��50�������EOF��_____�ȣ���FOH��_____�ȣ�
(2)����AFH+��CHF��100�������FOH�Ķ�����
����չ����ͼ�ڣ���AFH�͡�CHI��ƽ���߽��ڵ�O��EG������O��ƽ����FH���ֱ���AB��CD���ڵ�E��G������AFH+��CHF������ֱ��д����FOH�Ķ�����(�ú�a�Ĵ���ʽ��ʾ)
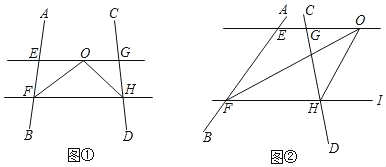
���𰸡���̽������1��30��125����2����FOH��130�㣻����չ����FOH��90�㩁![]() ����
����
��������
��1���ȸ��ݽ�ƽ���ߵĶ��������OFH����FHO �Ķ������ٸ��������ε��ڽǺͶ��������FOH�Ķ�����
��2���ȸ��ݽ�ƽ���ߵĶ��������OFH+��FHO �Ķ������ٸ��������ε��ڽǺͶ��������FOH�Ķ�����
����չ�� �ȸ��ݽ�ƽ���ߵĶ��������OFH��![]() ��AFH����OHI��
��AFH����OHI��![]() ��CHI��
��CHI��![]() ��180��-��CHF�����ٸ�����ֱ��ƽ���ڴ�����ȵ���FOH����OHI����OFH���ɡ�
��180��-��CHF�����ٸ�����ֱ��ƽ���ڴ�����ȵ���FOH����OHI����OFH���ɡ�
��1���ߡ�AFH��60����OFƽ�֡�AFH��
���OFH��30����
�֡�EG��FH��
���EOF����OFH��30������ֱ��ƽ���ڴ����������
�ߡ�CHF��50����OHƽ�֡�CHF��
���FHO��25����
���FOH�У���FOH��180������OFH����OHF��125���������ε��ڽǺͶ�������
�ʴ�Ϊ��30��125��
��2����FOƽ�֡�AFH��HOƽ�֡�CHF��
���OFH��![]() ��AFH����OHF��
��AFH����OHF��![]() ��CHF��
��CHF��
�ߡ�AFH+��CHF��100����
���OFH+��OHF��![]() ����AFH+��CHF����
����AFH+��CHF����![]() ��100����50����
��100����50����
��EG��FH��
���EOF����OFH����GOH����OHF����ֱ��ƽ���ڴ��������.
���EOF+��GOH����OFH+��OHF��50����
�ߡ�EOF+��GOH+��FOH��180���������ε��ڽǺͶ�������
���FOH��180��������EOF+��GOH ����180����50����130����
��չ�ߡ�AFH�͡�CHI��ƽ���߽��ڵ�O��
���OFH��![]() ��AFH����OHI��
��AFH����OHI��![]() ��CHI��
��CHI��
���FOH����OHI����OFH
��![]() ����CHI����AFH��
����CHI����AFH��
��![]() ��180������CHF����AFH��
��180������CHF����AFH��
��![]() ��180��������
��180��������
��90����![]() ����
����
��̽����
��1���ߡ�AFH��60�㣬OFƽ�֡�AFH��
���OFH��30�㣬
�֡�EG��FH��
���EOF����OFH��30�㣻
�ߡ�CHF��50�㣬OHƽ�֡�CHF��
���FHO��25�㣬
���FOH�У���FOH��180�㩁��OFH����OHF��125�㣻
�ʴ�Ϊ��30��125��
��2����FOƽ�֡�AFH��HOƽ�֡�CHF��
���OFH��![]() ��AFH����OHF��
��AFH����OHF��![]() ��CHF��
��CHF��
�ߡ�AFH+��CHF��100�㣬
���OFH+��OHF��![]() ����AFH+��CHF����
����AFH+��CHF����![]() ��100�㣽50�㣮
��100�㣽50�㣮
��EG��FH��
���EOF����OFH����GOH����OHF��
���EOF+��GOH����OFH+��OHF��50�㣮
�ߡ�EOF+��GOH+��FOH��180�㣬
���FOH��180�㩁����EOF+��GOH ����180�㩁50�㣽130�㣮
��չ�ߡ�AFH�͡�CHI��ƽ���߽��ڵ�O��
���OFH��![]() ��AFH����OHI��
��AFH����OHI��![]() ��CHI��
��CHI��
���FOH����OHI����OFH
��![]() ����CHI����AFH��
����CHI����AFH��
��![]() ��180�㩁��CHF����AFH��
��180�㩁��CHF����AFH��
��![]() ��180�㩁����
��180�㩁����
��90�㩁![]() ����
����


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У�AB��AC �� �ֱ��Ե�B�͵�CΪԲ�ģ�����BCһ��ij�Ϊ�뾶��Բ���������ཻ�ڵ�M�͵�N �� ��ֱ��MN��AB�ڵ�D������CD.��AB��7��AC��5�����ACD���ܳ�Ϊ�� ��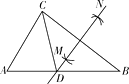
A.2 ![]()
B.12
C.17
D.19
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵxOy�У����κ���y=x2��2x+m��m��0���ĶԳ��������ϵ��Ϊ5�ķ���������ͼ���ڵ�A����x�ύ�ڵ�B�������ߵ�ͼ����y�ύ�ڵ�C����OC=3OB��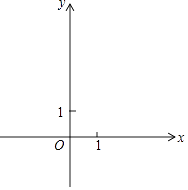
��1�����A�����ꣻ
��2����ֱ��AC�ı���ʽ��
��3����E��ֱ��AC��һ���㣬��F��x���Ϸ���ƽ���ڣ���ʹ��A��B��E��FΪ������ı��������Σ�ֱ��д����F�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����������̻�������˾�����Ƴ���У�̻�����������շѷ���.
��˾������ÿ�µ���������y��Ԫ�����̻����x��ƽ���ף���һ�κ�����ϵ����ͼ��ʾ.
�ҹ�˾�������̻����������1000ƽ����ʱ��ÿ����ȡ����5500Ԫ���̻��������1000ƽ����ʱ��ÿ������ȡ5500Ԫ�Ļ����ϣ���������ÿƽ������ȡ4Ԫ.

��1������ͼ��ʾ��y��x�ĺ�������ʽ������Ҫ��дȡֵ��Χ��
��2�����ijѧУĿǰ���̻������1200ƽ����.��ͨ������˵����ѡ���ļҹ�˾�ķ���ÿ�µ��̻��������ý���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���۲�������ʽ��������⣺
![]()
![]()
![]() ����
����
��1�������1 3 5 7 9 11�Ľ��Ϊ ��
�����1 3 5 7 9 29 �Ľ��Ϊ ��
��2����n ��ʾ�����������ú� n �Ĵ���ʽ��ʾ1 3 5 7 9 (2n 1) (2n 1) ��ֵΪ
��3�������������ɼ����� 41 43 45 77 79 ��ֵ��Ҫ��д����ϸ����������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����һ�ž���ֽƬABCD��EF�۵���A����CD���ϵĵ�A�䴦����B���ڵ�B�䴦������2=40�㣬��ͼ�С�1�Ķ���Ϊ�� �� 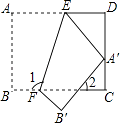
A.115��
B.120��
C.130��
D.140��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ʡij���ճ�Ϊȫ�˻������һ��ɱ�Ϊÿ��20Ԫ�Ĺ���Ʒ��Ͷ���г���������ÿ���������y���������ۼ�x��Ԫ/������һ�κ��������ۼ�Ϊ22Ԫ/��ʱ��ÿ��������Ϊ780�������ۼ�Ϊ25Ԫ/��ʱ��ÿ��������Ϊ750����
��1����y��x�ĺ�����ϵʽ��
��2������ù���Ʒ�ۼ���߲�����ÿ��30Ԫ����ô�ۼ۶�Ϊÿ������Ԫʱ�����ճ����۸ù���Ʒÿ���õ����������������Ƕ���Ԫ��������=�ۼ�-�ɱ���
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com