
【题目】如图,⊙O的半径OA⊥OC,点D在![]() 上,且
上,且![]() =2
=2![]() ,OA=4.
,OA=4.
(1)∠COD= °;
(2)求弦AD的长;
(3)P是半径OC上一动点,连结AP、PD,请求出AP+PD的最小值,并说明理由.
(解答上面各题时,请按题意,自行补足图形)

【答案】(1)30;(2)弦AD长为4;(3)AP+PD的最小值为![]() ,理由见解析.
,理由见解析.
【解析】(本小题满分12分)
解:(1)30;……………………………………………………………………1分
(2)连结OD、AD(如图2).
∵OA⊥OC,∴∠AOC=90°.∵![]() =2
=2![]() ,
,
设![]() 所对的圆心角∠COD=
所对的圆心角∠COD=![]() ,………………………………………………1分
,………………………………………………1分
则∠AOD=![]() ,…………………………………………………………………2分
,…………………………………………………………………2分
由∠AOD+∠DOC=90°,
得![]() +
+![]() =90°,∴
=90°,∴![]() =30°,
=30°,![]() =60°,…………………………3分
=60°,…………………………3分
即∠AOD=60°,又∵OA=OD,∴△AOD为等边三角形,…………4分
∴AD=OA=4;…………………………………………………………………5分
(3)过点D作DE⊥OC,交⊙O于点E,……………………………………1分
连结AE,交OC于点P(如图3),………………………………………………2分
则此时,AP+PD的值最小.
∵根据圆的对称性,点E是点D关于OC的对称点,
OC是DE的垂直平分线,即PD=PE.………………………………………3分
∴AP+PD=AP+PE=AE,
若在OC上另取一点F,连结AF、FD及EF,
在△AFE中,AF+FE>AE,
即AF+FE>AP+PD,
∴可知AP+PD最小.…………………………………………………………4分
∵∠AED=![]() ∠AOD=30°,
∠AOD=30°,
又∵OA⊥OC,DE⊥OC,∴OA∥DE,
∴∠OAE=∠AED=30°.
延长AO交⊙O于点B,连结BE,∵AB为直径,
∴△ABE为直角三角形.由![]() =cos∠BAE,……………………………5分
=cos∠BAE,……………………………5分
得AE=AB·cos30°=2×4×![]() =
=![]() ,……………………………6分
,……………………………6分
即AP+PD=![]() ,
,
[也可利用勾股定理求得AE]


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,菱形EFGH的三个顶点E、G、H分别在正方形ABCD的边AB、CD、DA上,连接CF.
(1)求证:∠HEA=∠CGF;
(2)当AH=DG时,求证:菱形EFGH为正方形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长是4,∠DAC的角平分线交DC于点E,点P、Q分别是边AD和AE上的动点(两动点不重合).
(1)PQ+DQ的最小值是 .
(2)说出PQ+DQ取得最小值时,点P、Q的位置,并在图中画出;
(3)请对(2)中你所给的结论进行证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数![]() =
=![]() +
+![]() +
+![]() 的顶点M是直线
的顶点M是直线![]() =-
=-![]() 和直线
和直线![]() =
=![]() +
+![]() 的交点.
的交点.
(1)若直线![]() =
=![]() +
+![]() 过点D(0,-3),求M点的坐标及二次函数
过点D(0,-3),求M点的坐标及二次函数![]() =
=![]() +
+![]() +
+![]() 的解析式;
的解析式;
(2)试证明无论![]() 取任何值,二次函数
取任何值,二次函数![]() =
=![]() +
+![]() +
+![]() 的图象与直线
的图象与直线![]() =
=![]() +
+![]() 总有两个不同的交点;
总有两个不同的交点;
(3)在(1)的条件下,若二次函数![]() =
=![]() +
+![]() +
+![]() 的图象与
的图象与![]() 轴交于点C,与
轴交于点C,与![]() 的右交点为A,试在直线
的右交点为A,试在直线![]() =-
=-![]() 上求异于M的点P,使P在△CMA的外接圆上.
上求异于M的点P,使P在△CMA的外接圆上.
查看答案和解析>>
科目:初中数学 来源: 题型:
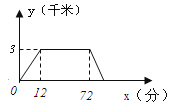
【题目】小明从家里出发到超市买东西,再回到家,他离家的距离y(千米)与时间t(分钟)的关系如图所示.请你根据图象回答下列问题:
(1)小明家离超市的距离是 千米;
(2)小明在超市买东西时间为 小时;
(3)小明去超市时的速度是 千米/小时.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com