
【题目】二次函数![]() =
=![]() +
+![]() +
+![]() 的顶点M是直线
的顶点M是直线![]() =-
=-![]() 和直线
和直线![]() =
=![]() +
+![]() 的交点.
的交点.
(1)若直线![]() =
=![]() +
+![]() 过点D(0,-3),求M点的坐标及二次函数
过点D(0,-3),求M点的坐标及二次函数![]() =
=![]() +
+![]() +
+![]() 的解析式;
的解析式;
(2)试证明无论![]() 取任何值,二次函数
取任何值,二次函数![]() =
=![]() +
+![]() +
+![]() 的图象与直线
的图象与直线![]() =
=![]() +
+![]() 总有两个不同的交点;
总有两个不同的交点;
(3)在(1)的条件下,若二次函数![]() =
=![]() +
+![]() +
+![]() 的图象与
的图象与![]() 轴交于点C,与
轴交于点C,与![]() 的右交点为A,试在直线
的右交点为A,试在直线![]() =-
=-![]() 上求异于M的点P,使P在△CMA的外接圆上.
上求异于M的点P,使P在△CMA的外接圆上.
【答案】(1)M点坐标为M(2,-1),二次函数![]() =
=![]() +
+![]() +
+![]() 的解析式为:
的解析式为: ![]() =
=![]() -4
-4![]() +3;
+3;
(2)证明见解析;
(3)P(-![]() ,
, ![]() )
)
【解析】(本小题满分14分)
解:(1)把D(0,-3)坐标代入直线![]() =
=![]() +
+![]() 中,
中,
得![]() =-3,从而得直线
=-3,从而得直线![]() =
=![]() -3.……………………………………………1分
-3.……………………………………………1分
由M为直线![]() =-
=-![]() 与直线
与直线![]() =
=![]() -3的交点,
-3的交点,
得 ,………………………………………………………………………2分
,………………………………………………………………………2分
解得![]() ,∴得M点坐标为M(2,-1).…………………………………3分
,∴得M点坐标为M(2,-1).…………………………………3分
∵M为二次函数![]() =
=![]() +
+![]() +
+![]() 的顶点,∴其对称轴为
的顶点,∴其对称轴为![]() =2,
=2,
由对称轴公式: ![]() =-
=-![]() ,得-
,得-![]() =2,∴
=2,∴![]() =-4;
=-4;
由![]() =-1,得
=-1,得![]() =-1,得
=-1,得![]() =3.
=3.
∴二次函数![]() =
=![]() +
+![]() +
+![]() 的解析式为:
的解析式为: ![]() =
=![]() -4
-4![]() +3;………………4分
+3;………………4分
[也可用顶点式求得解析式:由M(2,-1),
得![]() =
=![]() -1,展开得
-1,展开得![]() =
=![]() -4
-4![]() +3]
+3]
(2)∵M是直线![]() =-
=-![]() 和
和![]() =
=![]() +
+![]() 的交点,得
的交点,得 ,
,
解得 ,∴得M点坐标为M(-
,∴得M点坐标为M(-![]() ,
, ![]() ).…………………………1分
).…………………………1分
从而有-![]() =-
=-![]() 和
和 =
=![]() ,
,
解得![]() =
=![]() ;
; ![]() =
=![]() +
+![]() .…………………………………………………3分
.…………………………………………………3分
由![]() ,得
,得![]() +(
+(![]() -1)
-1)![]() +
+![]() -
-![]() =0,……………………4分
=0,……………………4分
该一元二次方程根的判别式
⊿=(![]() -1)2-4(
-1)2-4(![]() -
-![]() )
)
=(![]() -1)2-4(
-1)2-4(![]() +
+![]() -
-![]() )=1>0,…………………………5分
)=1>0,…………………………5分
∴二次函数![]() =
=![]() +
+![]() +
+![]() 的图象与直线
的图象与直线![]() =
=![]() +
+![]() 总有两个不同的交点;
总有两个不同的交点;
(3)解法①:
由(1)知,二次函数的解析式为: ![]() =
=![]() -4
-4![]() +3,
+3,
当![]() =0时,
=0时, ![]() =3.∴点C的坐标为C(0,3).……………………………1分
=3.∴点C的坐标为C(0,3).……………………………1分
令![]() =0,即
=0,即![]() -4
-4![]() +3=0,解得
+3=0,解得![]() =1,
=1, ![]() =3,
=3,
∴点A的坐标为A(3,0).………………………………………………………2分
由勾股定理,得AC=3![]() .∵M点的坐标为M(2,-1),
.∵M点的坐标为M(2,-1),
过M点作![]() 轴的垂线,垂足的坐标应为(2,0),由勾股定理,
轴的垂线,垂足的坐标应为(2,0),由勾股定理,
得AM=![]() ;过M点作
;过M点作![]() 轴的垂线,垂足的坐标应为(0,-1),
轴的垂线,垂足的坐标应为(0,-1),
由勾股定理,得CM=![]() =
=![]() =2
=2![]() .
.
∵AC2+AM2=20=CM2,∴△CMA是直角三角形,……………………3分
CM为斜边,∠CAM=90°.
直线![]() =-
=-![]() 与△CMA的外接圆的一个交点为M,另一个交点为P,
与△CMA的外接圆的一个交点为M,另一个交点为P,
则∠CPM=90°.即△CPM为Rt△.………………………………………4分
设P点的横坐标为![]() ,则P(
,则P(![]() ,-
,- ![]() ).过点P作
).过点P作![]() 轴垂线,
轴垂线,
过点M作![]() 轴垂线,两条垂线交于点E(如图4),则E(
轴垂线,两条垂线交于点E(如图4),则E(![]() ,-1).
,-1).
过P作PF⊥![]() 轴于点F,则F(0,-
轴于点F,则F(0,- ![]() ).
).
在Rt△PEM中,PM2=PE2+EM2
=(-![]() +1)2+(2-
+1)2+(2-![]() )2=
)2=![]() -5
-5![]() +5.
+5.
在Rt△PCF中,PC2=PF2+CF2=![]() +(3+
+(3+![]() )2
)2
=![]() +3
+3![]() +9.在Rt△PCM中,PC2+PM2=CM2,
+9.在Rt△PCM中,PC2+PM2=CM2,
得![]() +3
+3![]() +9+
+9+![]() -5
-5![]() +5=20,
+5=20,
化简整理得5![]() -4
-4![]() -12=0,解得
-12=0,解得![]() =2,
=2, ![]() =-
=-![]() .
.
当![]() =2时,
=2时, ![]() =-1,即为M点的横、纵坐标.
=-1,即为M点的横、纵坐标.
∴P点的横坐标为-![]() ,纵坐标为
,纵坐标为![]() .
.
∴P(-![]() ,
, ![]() ).……………………………………………………………………5分
).……………………………………………………………………5分
解法②[运用现行高中基本知识(解析几何):线段中点公式及两点间距离公式]:
设线段CM的中点(即△CMA内接圆的圆心)为H,则由线段中点公式,可求出H的坐标为H(1,1).∵点P在⊙H上,∴点P到圆心H的距离等于半径.
设点P的坐标为:P(![]() ,-
,- ![]() ),由两点间的距离公式,得PH的长度为:
),由两点间的距离公式,得PH的长度为:
 ,从而有:
,从而有:  =
=![]() ,即
,即
![]() =5,化简,整理,得化简整理得5
=5,化简,整理,得化简整理得5![]() -4
-4![]() -12=0,解得
-12=0,解得![]() =2,
=2, ![]() =-
=-![]() .当
.当![]() =2时,
=2时, ![]() =-1,即为M点的横、纵坐标.
=-1,即为M点的横、纵坐标.
∴P点的横坐标为-![]() ,纵坐标为
,纵坐标为![]() .
.
∴P(-![]() ,
, ![]() ).
).


科目:初中数学 来源: 题型:
【题目】某校要从小王和小李两名同学中挑选一人参加全市知识竞赛,在最近的五次选拔测试中,他俩的成绩分别如下表:
次数 | 1 | 2 | 3 | 4 | 5 |
小王 | 60 | 75 | 100 | 90 | 75 |
小李 | 70 | 90 | 100 | 80 | 80 |
根据上表解答下列问题:
(1)完成下表:
姓名 | 平均成绩(分) | 中位数(分) | 众数(分) | 方差 |
小王 | 80 | 75 | 75 | 190 |
小李 |
(2)在这五次测试中,成绩比较稳定的同学是谁?若将80分以上(含80分)的成绩视为优秀,则小王、小李在这五次测试中的优秀率各是多少?
(3)历届比赛表明,成绩达到80分以上(含80分)就很可能获奖,成绩达到90分以上(含90分)就很可能获得一等奖,那么你认为选谁参加比赛比较合适?说明你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某村原有林地108公顷,旱地54公顷,为保护环境,需把一部分旱地改造为林地,使旱地面积占林地面积的20%.设把x公顷旱地改为林地,则可列方程( )
A.54﹣x=20%×108
B.54﹣x=20%(108+x)
C.54+x=20%×162
D.108﹣x=20%(54+x)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O的半径OA⊥OC,点D在![]() 上,且
上,且![]() =2
=2![]() ,OA=4.
,OA=4.
(1)∠COD= °;
(2)求弦AD的长;
(3)P是半径OC上一动点,连结AP、PD,请求出AP+PD的最小值,并说明理由.
(解答上面各题时,请按题意,自行补足图形)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把下列各数分别填入相应的集合内:
﹣2.5,0,8,﹣2, ![]() ,
, ![]() , ﹣0.5252252225…(每两个5之间依次增加1个2).
, ﹣0.5252252225…(每两个5之间依次增加1个2).
(1)正数集合:{ …};
(2)负数集合:{ …};
(3)整数集合:{ …};
(4)无理数集合:{ …}.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合题。
(1)如图1,在△ABC中,AB=AC,CD⊥AB于D,BE⊥AC于E,试证明:CD=BE.
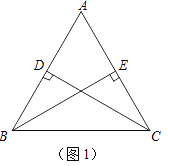
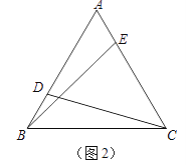
(2)如图2,在△ABC中,仍然有条件“AB=AC,点D,E分别在AB和AC上”.若∠ADC+∠AEB=180°,则CD与BE是否仍相等?若相等,请证明;若不相等,请举反例说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小敏从A地出发向B地行走,同时小聪从B地出发向A地行走,如图所示,相交于点P的两条线段l1、l2分别表示小敏、小聪离B地的距离y(km)与已用时间x(h)之间的关系,则小敏、小聪行走的速度分别是( )
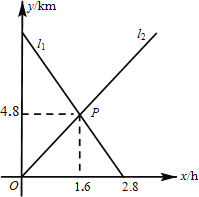
A. 3km/h和4km/h B. 3km/h和3km/h
C. 4km/h和4km/h D. 4km/h和3km/h
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年参加我市初中毕业生学业考试的总人数约为56000人,这个数据用科学记数法表示为( )
A.5.6×103
B.5.6×104
C.5.6×105
D.0.56×105
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com