
【题目】综合题。
(1)如图1,在△ABC中,AB=AC,CD⊥AB于D,BE⊥AC于E,试证明:CD=BE.
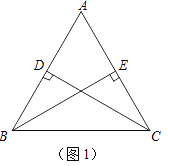
(2)如图2,在△ABC中,仍然有条件“AB=AC,点D,E分别在AB和AC上”.若∠ADC+∠AEB=180°,则CD与BE是否仍相等?若相等,请证明;若不相等,请举反例说明.
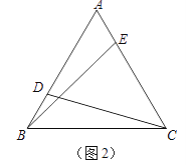
【答案】(1)证明见解析(2)CD=BE
【解析】试题分析:(1)利用AAS证明△ABE≌△ACD,利用全等三角形的性质即可证得结论;(2)分别作CF⊥AB,BG⊥AC,CD=BE,利用AAS证明△FBC≌△GCB,根据全等三角形的对应边相等可得CF=BG;再证得∠ADC=∠BEG,利用AAS证明△CFD≌△BGE,根据全等三角形的对应边相等即可得结论.
试题解析:
(1)证明:∵CD⊥AB于点D,BE⊥AC,
∴∠AEB=∠ADC=90°,
在△ABE与△ACD中, 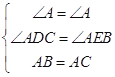 ,
,
∴△ABE≌△ACD(AAS).
∴CD=BE
(2)CD=BE, 证明如下:分别作CF⊥AB,BG⊥AC,
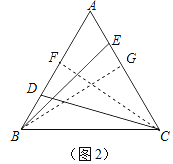
∴∠CBF=90°,∠BGC=90°,
∵AB=AC,
∴∠ABC=∠ACB,
在△FBC和△GCB中, 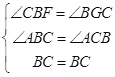 ,
,
∴△FBC≌△GCB.
∴CF=BG,
∵∠ADC+∠AEB=180°,
又∵∠BEG+∠AEB=180°,
∴∠ADC=∠BEG,
在△CFD和△BGE中, 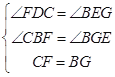 ,
,
∴△CFD≌△BGE,
∴CD=BE.


 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案科目:初中数学 来源: 题型:
【题目】二次函数![]() =
=![]() +
+![]() +
+![]() 的顶点M是直线
的顶点M是直线![]() =-
=-![]() 和直线
和直线![]() =
=![]() +
+![]() 的交点.
的交点.
(1)若直线![]() =
=![]() +
+![]() 过点D(0,-3),求M点的坐标及二次函数
过点D(0,-3),求M点的坐标及二次函数![]() =
=![]() +
+![]() +
+![]() 的解析式;
的解析式;
(2)试证明无论![]() 取任何值,二次函数
取任何值,二次函数![]() =
=![]() +
+![]() +
+![]() 的图象与直线
的图象与直线![]() =
=![]() +
+![]() 总有两个不同的交点;
总有两个不同的交点;
(3)在(1)的条件下,若二次函数![]() =
=![]() +
+![]() +
+![]() 的图象与
的图象与![]() 轴交于点C,与
轴交于点C,与![]() 的右交点为A,试在直线
的右交点为A,试在直线![]() =-
=-![]() 上求异于M的点P,使P在△CMA的外接圆上.
上求异于M的点P,使P在△CMA的外接圆上.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题中,假命题是( )
A. 菱形的面积等于两条对角线乘积的一半
B. 矩形的对角线相等
C. 对角线互相垂直的平行四边形是矩形
D. 对角线相等的菱形是正方形
查看答案和解析>>
科目:初中数学 来源: 题型:
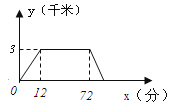
【题目】小明从家里出发到超市买东西,再回到家,他离家的距离y(千米)与时间t(分钟)的关系如图所示.请你根据图象回答下列问题:
(1)小明家离超市的距离是 千米;
(2)小明在超市买东西时间为 小时;
(3)小明去超市时的速度是 千米/小时.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() (a≠0)的图象如图所示,该抛物线与x轴的一个交点(-1,0)为请回答以下问题
(a≠0)的图象如图所示,该抛物线与x轴的一个交点(-1,0)为请回答以下问题
(1)求抛物线与x轴的另一个交点坐标
(2)一元二次方程![]() 的解为
的解为
(3)不等式![]() 的解集是
的解集是

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com