
【题目】已知x=![]() ,求x6+x5+2x4-4x3+3x2+4x-4的整数部分.
,求x6+x5+2x4-4x3+3x2+4x-4的整数部分.
【答案】36
【解析】试题分析:根据算术平方根为非负数判断出x>0,然后利用放缩法判断出![]() 与
与![]() 都不成立,从而得到
都不成立,从而得到![]() ,两边平方得到x2-x-1=0,根据一元二次方程的解法求出x的值,再利用配项法把x6+x5+2x4-4x3+3x2+4x-4整理成(x2-x-1)与另一多项式相乘的形式加上另一多项式,然后代入x的值进行计算,最后利用“夹逼法”进行解答.
,两边平方得到x2-x-1=0,根据一元二次方程的解法求出x的值,再利用配项法把x6+x5+2x4-4x3+3x2+4x-4整理成(x2-x-1)与另一多项式相乘的形式加上另一多项式,然后代入x的值进行计算,最后利用“夹逼法”进行解答.
试题解析:由已知得x>0,
若![]() >x,
>x,
则x=![]() >
>![]() >
>![]() ,与假设矛盾;
,与假设矛盾;
若![]() <x,
<x,
则x=![]() <
<![]() <
<![]() ,与假设矛盾;
,与假设矛盾;
因此![]() =x,
=x,
两边平方并整理得,x2-x-1=0,
解得x= ![]() ,x=
,x=![]() (舍去),
(舍去),
而x6+x5+2x4-4x3+3x2+4x-4=(x6-x5-x4)+(2x5-2x4-2x3)+(5x4-5x3-5x2)+(3x3-3x2-3x)+(11x2-11x-11)+18x+7,
=x4(x2-x-1)+2x3(x2-x-1)+5x2(x2-x-1)+3x(x2-x-1)+11x(x2-x-1)+18x+7,
=(x2-x-1)(x4+2x3+5x2+3x+11)+18x+7,
=18x+7,
所以,原式=18×![]() +7=16+9
+7=16+9![]() =16+
=16+![]() ,
,
∵20<![]() <21,
<21,
∴所求整数值为36.


科目:初中数学 来源: 题型:
【题目】如图,⊙O的半径OA⊥OC,点D在![]() 上,且
上,且![]() =2
=2![]() ,OA=4.
,OA=4.
(1)∠COD= °;
(2)求弦AD的长;
(3)P是半径OC上一动点,连结AP、PD,请求出AP+PD的最小值,并说明理由.
(解答上面各题时,请按题意,自行补足图形)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小敏从A地出发向B地行走,同时小聪从B地出发向A地行走,如图所示,相交于点P的两条线段l1、l2分别表示小敏、小聪离B地的距离y(km)与已用时间x(h)之间的关系,则小敏、小聪行走的速度分别是( )
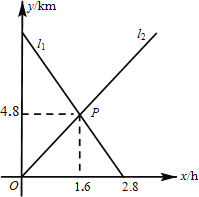
A. 3km/h和4km/h B. 3km/h和3km/h
C. 4km/h和4km/h D. 4km/h和3km/h
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】国庆节期间,某文具店平均每天可卖出300张贺卡,卖出1张贺卡的利润是1元.经调查发现,零售单价每降0.1元,每天可多卖出100张贺卡.为了使每天获取的利润更多,该店决定把零售单价下降![]() 元.
元.
(1)零售单价下降![]() 元后,该店平均每天可卖出___________张贺卡,每张贺卡的利润为___________元;(用含
元后,该店平均每天可卖出___________张贺卡,每张贺卡的利润为___________元;(用含![]() 的式子表示)
的式子表示)
(2)在不考虑其他因素的条件下,该店希望每天卖贺卡获得的利润是420元,并且能卖出更多的贺卡赢得市场,![]() 应定为多少?
应定为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年参加我市初中毕业生学业考试的总人数约为56000人,这个数据用科学记数法表示为( )
A.5.6×103
B.5.6×104
C.5.6×105
D.0.56×105
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知A、B两地的路程为240千米.某经销商每天都要用汽车或火车将x吨保鲜品一次 性由A地运往B地.受各种因素限制,下一周只能采用汽车和火车中的一种进行运输,且须提前预订.
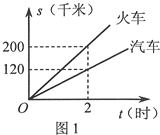
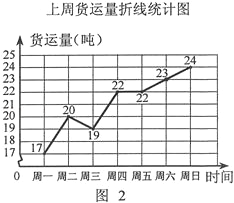
现有货运收费项目及收费标准表、行驶路程s(千米)与行驶时间t(时)的函数图象(如图1)、上周货运量折线统计图(如图2)等信息如下:
货运收费项目及收费标准表
运输工具 | 运输费单价 元/(吨千米) | 冷藏费单价 元/(吨时) | 固定费用 元/次 |
汽车 | 2 | 5 | 200 |
火车 | 1.6 | 5 | 2280 |
(1)汽车的速度为 千米/时,火车的速度为 千米/时:
(2)设每天用汽车和火车运输的总费用分别为y汽(元)和y火(元),分别求y汽、y火与 x的函数关系式(不必写出x的取值范围),及x为何值时y汽>y火 (总费用=运输费+冷藏费+固定费用)
(3)请你从平均数、折线图走势两个角度分析,建议该经销商应提前为下周预定哪种运输工具,才能使每天的运输总费用较省?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com