如图，O是等边三角形ABC内一
点，∠AOB=110°，∠BOC=α，D是△ABC外一点，且△ADC≌△BOC，连接OD．
(1) 求证：ACOD是等边三角形；
(2) 当α=150°时，试判断△AOD的形状，并说明理由；
(3) 当α为多少度时，△AOD是等腰三角形?
(1) ∵△ADC≌△BOC，∴DC=OC，∠DCA=∠OCB．∵△ABC为等边三角形，∴∠OC
B+∠ACO=∠ACB=60°．∴∠DCA+∠ACO=∠DCO=60°．∴△COD是等边三角形 (2) 当α=150°时，△AOD是直角三角形 理由：∵△ADC≌△BOC，∴∠ADC=∠BOC=150°．又∵△COD是等边三角形，∴∠ODC=60°．∴∠ADO=90。，即△AOD是直角三角形． (3) ① 要使AO=AD，需∠AOD=∠ADO．∵∠AOD=190°－α，∠ADO=α－60°，∴190°－α=α－60°，∴α=125°．② 要使OA=OD，需∠OAD=∠ADO.∵∠OAD=180°－(∠AOD+∠ADO)=180°－(190°－α+α－60°)=50°，∴α－60°－50°．∴α=110°．③要使AD=OD，需∠AOD=∠OAD，∴190°－α=50°．∴α=140°．
综上所述，当α为125°，110°或140°时，△AOD是等腰三角形．
科目：初中数学 来源： 题型：
已
知△ABC的三条边长分别为3，4，6，在△ABC所在平面内画一条直线，将△ABC分割成两个三角形，使其中的一个是等腰三角形，则这样的直线最多可
画 ( )
A．6条 B．
7条 C．8条 D．9条
查看答案和解析>>
科目：初中数学 来源： 题型：
点P为∠AOB内一点，∠AOB=30°，P关于OA，OB的对称点分别为M，N，则△MON定是 ( )
A．等边三角形 B．等腰三角形 C．直角三角形 D．等腰直角三角形
查看答案和解析>>
科目：初中数学 来源： 题型：
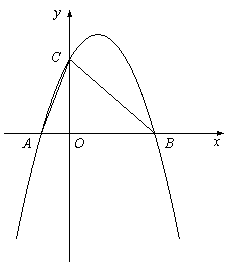
如图，二次函数y=－x 2＋bx＋c与x轴交于A（－1,0）、B（3,0）两点，与y轴交于点C．
（1）求抛物线的解析式及其对称轴；
（2）将抛物线沿y轴向下平移m（m ＞0）个单位，当平移后的抛物线与线段OB有且只有一个交点时，求m的取值范围或m的值；
（3）抛物线上是否存在点M，使∠BCM＝∠BAC－∠ACO，若存在，求M点坐标；若不存在，说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
下列语句中，正确的有( ) 
．1个 
．2个 
．3个 
．4个
①相等的
圆心角所对的弧相等；②平分弦的直径垂直于弦；③长度相等的两条弧
是等弧；④经过圆心的每一条直线都是圆的对称轴．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
．PC≤PD D．不能确定
