练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    5．给出下列各式：$\frac{x+y}{2}$，$\frac{y}{x-1}$，$\frac{x}{π}$，-$\frac{n}{m}$，其中，分式有（　　）
    A．4个B．3个C．2个D．1个

    分析 判断分式的依据是看分母中是否含有字母，如果含有字母则是分式，如果不含有字母则不是分式．

    解答 解：$\frac{x+y}{2}$，$\frac{x}{π}$，的分母中均不含有字母，因此它们是整式，而不是分式；
    $\frac{y}{x-1}$-$\frac{n}{m}$分母中含有字母，因此是分式；
    故选：C．

    点评 本题主要考查分式的定义，注意π不是字母，是常数，所以$\frac{x}{π}$不是分式，是整式．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    15．若一直角三角形两边长为4和5，则第三边长为（　　）
    A．3B．$\sqrt{41}$C．3或$\sqrt{41}$D．不确定

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    16．如图，⊙O的直径AB=8，∠CBD=30°，则CD等于（　　）
    A．1B．2C．3D．4

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

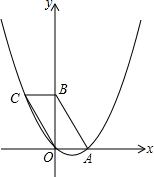    13．已知，如图，把平行四边形OABC放置于平面直角坐标系中，OA落在x轴的正半轴上，OB落在y轴的正半轴上，OA=2，OB=4，抛物线y=ax2+bx+c经过A、O、C三点．
    （1）求该抛物线的解析式；
    （2）试问在抛物线的对称轴上是否存在一点T，使得|TO-TC|的值最大？若存在，求出T点的坐标，若不存在，请说明理由；
    （3）已知点P为抛物线在第一象限内上的一个动点，点Q为x轴上任意一点，若以O、P、Q为顶点的三角形与△OBC相似，请求出点Q的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    20．已知（x1，y1），（x2，y2），（x3，y3）是反比例函数y=-$\frac{4}{x}$的图象上的三个点，且x1＜0，x2＞x3＞0，则y1，y2，y3的大小关系是y1＞y2＞y3．（用“＞”表示）

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    10．如图，在平面直角坐标系中，四边形OABC是菱形，若点A坐标为（4，3），则菱形ABCD的面积是24，周长是20．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    17．定义运算a?b=a（1-b），下列给出了关于这种运算的几个结论：
    ①2?（-2）=6；②a?b=b?a；③若a+b=0，则（a?a）+b（b?b）=2ab；④若a?b=0，则a=0或b=1，其中正确结论的序号是①④．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

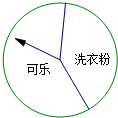    14．某商场“五一”期间为进行有奖销售活动，设立了一个可以自由转动的转盘．商场规定：顾客购物100元以上就能获得一次转动转盘的机会，当转盘停止时，指针落在哪一区域就可以获得相应的奖品．下表是此次活动中的一组统计数据：
    转动转盘的次数n1002004005008001000
    落在“可乐”区域的次数m60122240298604
    落在“可乐”区域的频率$\frac{m}{n}$0.60.610.60.590.604
    （1）完成上述表格；（结果全部精确到0.1）
    （2）请估计当n很大时，频率将会接近0.6，假如你去转动该转盘一次，你获得“可乐”的概率约是0.6；（结果全部精确到0.1）
    （3）转盘中，表示“洗衣粉”区域的扇形的圆心角约是多少度？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    15．计算：$\sqrt{27}$-|1-tan60°|-（2cos45°-1）0-4sin60°．

    查看答案和解析>>

    同步练习册答案