
【题目】在一个不透明的口袋里装有只有颜色不同的黑、白两种颜色的球共20只,某学习小组做摸球实验,将球搅匀后从中随机摸出一个球记下颜色,再把它放回袋中,不断重复.下表是活动进行中的一组统计数据:
摸球的次数n | 100 | 150 | 200 | 500 | 800 | 1000 |
摸到白球的次数m | 59 | 96 | 116 | 290 | 480 | 601 |
摸到白球的频率 | a | 0.64 | 0.58 | b | 0.60 | 0.601 |
(1)上表中的a= ;b=
(2)“摸到白球”的概率的估计值是 (精确到0.1);
(3)试估算口袋中黑、白两种颜色的球各有多少只?
科目:初中数学 来源: 题型:
【题目】有![]() 箱桔子,以每箱
箱桔子,以每箱![]() 千克为标准,称重记录如下(单位:千克,超过标准的千克数为正数,不足标准的千克数记为负数):
千克为标准,称重记录如下(单位:千克,超过标准的千克数为正数,不足标准的千克数记为负数):![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
![]() 称得的
称得的![]() 箱总质量与标准总质量相比超过或不足多少千克?
箱总质量与标准总质量相比超过或不足多少千克?
![]() 若每箱桔子进价
若每箱桔子进价![]() 元/千克,售价
元/千克,售价![]() 元/千克,则这
元/千克,则这![]() 箱桔子全部售出共盈利多少钱?
箱桔子全部售出共盈利多少钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中(请补画出必要的图形),![]() 为坐标原点,直线y=-2x+4与
为坐标原点,直线y=-2x+4与![]() 、
、![]() 轴分别交于
轴分别交于![]() 、
、![]() 两点,过线段
两点,过线段![]() 的中点
的中点![]() 作
作![]() 轴的垂线
轴的垂线![]() ,分别与直线
,分别与直线![]() 交于点
交于点![]() ,与直线y=x+n交于点
,与直线y=x+n交于点![]() .
.
(1)直接写出点A、B、C、![]() 的坐标:A(____________),B(____________),C(_____________),D(____________);
的坐标:A(____________),B(____________),C(_____________),D(____________);

(2)若![]() 的面积等于1,求点P的坐标.
的面积等于1,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知数轴上三点M,O,N对应的数分别为-1,0,3,点P为数轴上任意一点,其对应的数为x.
![]()
(1)MN的长为 ;
(2)如果点P到点M、点N的距离相等,那么x的值是 ;
(3)数轴上是否存在点P,使点P到点M、点N的距离之和是8?若存在,直接写出x的值;若不存在,请说明理由.
(4)如果点P以每分钟1个单位长度的速度从点O向左运动,同时点M和点N分别以每分钟2个单位长度和每分钟3个单位长度的速度也向左运动.设t分钟时点P到点M、点N的距离相等,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC三个顶点都在5×5的网格(每个小正方形的边长均为1个单位长度)的格点上,将△ABC绕点C顺时针旋转到△A′B′C的位置,且A′、B′仍落在格点上,则线段AC扫过的扇形所围成的圆锥体的底面半径是单位长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】长方形OABC,O为平面直角坐标系的原点,OA=5,OC=3,点B在第三象限.
(1)求点B的坐标;
(2)如图1,若过点B的直线BP与长方形OABC的边交于点P,且将长方形OABC的面积分为1:4两部分,求点P的坐标;
(3)如图2,M为x轴负半轴上一点,且∠CBM=∠CMB,N是x轴正半轴上一动点,∠MCN的平分线CD交BM的延长线于点D,在点N运动的过程中,![]() 的值是否变化?若不变,求出其值;若变化,请说明理由.
的值是否变化?若不变,求出其值;若变化,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下面的变形规律:
![]() ;
;![]() ;
;![]() ;….
;….
解答下面的问题:
(1)仿照上面的格式请写出![]() = ;
= ;
(2)若n为正整数,请你猜想![]() = ;
= ;
(3)基础应用:计算:![]() .
.
(4)拓展应用1:解方程:![]() =2016
=2016
(5)拓展应用2:计算:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为支持抗震救灾,我市A、B两地分别有赈灾物资100吨和180吨,需全部运往重灾区C、D两县,根据灾区的情况,这批赈灾物资运往C县的数量比运往D县的数量的2倍少80吨.
(1)求这批赈灾物资运往C、D两县的数量各是多少吨?
(2)设A地运往C县的赈灾物资数量为x吨(x为整数).若要B地运往C县的赈灾物资数量大于A地运往D县赈灾物资数量的2倍,且要求B地运往D县的赈灾物资数量不超过63吨,则A、B两地的赈灾物资运往C、D两县的方案有几种?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,∠A=60°,AC=a,作斜边AB边中线CD,得到第一个三角形ACD;DE⊥BC于点E,作Rt△BDE斜边DB上中线EF,得到第二个三角形DEF;依此作下去…则第n个三角形的面积等于 . 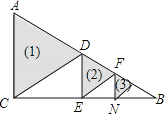
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com