
如图,Rt△ABC中,∠ABC=90°,以AB为直径作半圆⊙O交AC与点D,点E为BC的中点,连接DE.

(1)求证:DE是半圆⊙O的切线.
(2)若∠BAC=30°,DE=2,求AD的长.
见解析
【解析】
试题分析:(1)连结OD,根据条件证明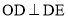 即可;(2)根据条件可得BC=2DE=4,Rt△ABC中,先由∠BAC=30°,得AC=2 BC =8,再根据条件可证△EDC为等边三角形,可得出DC=2, AD=AC-CD=6.
即可;(2)根据条件可得BC=2DE=4,Rt△ABC中,先由∠BAC=30°,得AC=2 BC =8,再根据条件可证△EDC为等边三角形,可得出DC=2, AD=AC-CD=6.
试题解析:(1)证明:连接OD,OE,
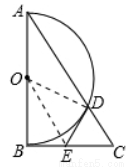
∵AB为圆O的直径,∴∠ADB=∠BDC=90°,在Rt△BDC中,E为斜边BC的中点,∴DE=BE,
在△OBE和△ODE中,OB=OD,OE=OE,BE=DE,∴△OBE≌△ODE(SSS),∴∠ODE=∠ABC=90°,所以DE为圆O的切线;
(2)在Rt△ABC中,∠BAC=30°,∴BC= 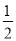 AC,∵BC=2DE=4,∴AC=8,又∵∠C=60°,DE=DC,∴△DEC为等边三角形,即DC=DE=2,所以AD=AC-DC=6.
AC,∵BC=2DE=4,∴AC=8,又∵∠C=60°,DE=DC,∴△DEC为等边三角形,即DC=DE=2,所以AD=AC-DC=6.
考点:1.切线的判定;2.直角三角形的性质;3. 等边三角形的判定与性质.


 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案科目:初中数学 来源:2014-2015学年江苏省盐城市阜宁县九年级上学期期中学情调研数学试卷(解析版) 题型:解答题
(本题12分)射线QN与等边△ABC的两边AB,BC分别交于点M,N,且AC∥QN,AM=MB=2cm,
QM=4cm.动点P从点Q出发,沿射线QN以每秒1cm的速度向右移动,经过t秒,以点P为圆心,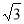 cm
cm
为半径的圆与△ABC的边相切(切点在边上),求t值(单位:秒).
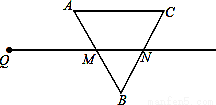
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省盐城市阜宁县九年级上学期期中学情调研数学试卷(解析版) 题型:填空题
若关于x的一元二次方程kx2﹣2x﹣1=0有两个不相等的实数根,则实数k的取值范围是
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省盐城市阜宁县九年级上学期期中学情调研数学试卷(解析版) 题型:选择题
在2012﹣2013NBA整个常规赛季中,科比罚球投篮的命中率大约是83.3%,下列说法错误的是( )
A.科比罚球投篮2次,一定全部命中
B.科比罚球投篮2次,不一定全部命中
C.科比罚球投篮1次,命中的可能性较大
D.科比罚球投篮1次,不命中的可能性较小
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省兴化顾庄等三校九年级上学期12月月考数学试卷(解析版) 题型:解答题
如图,有一路灯杆AB(底部B不能直接到达),在灯光下,小明在点D处测得自己的影长DF=3m,
沿BD方向到达点F处再测得自己的影长FG=4m.如果小明的身高为1.6m,求路灯杆AB的高度.

查看答案和解析>>
科目:初中数学 来源:2014-2015学年福建省九年级上学期第三次教学质量监测数学试卷(解析版) 题型:解答题
(本题满分10分)Rt△ABC与Rt△FED是两块全等的含30o、60o角的三角板,按如图(一)所示拼在一起,CB与DE重合.


(1)求证:四边形ABFC为平行四边形;
(2)取BC中点O,将△ABC绕点O顺时钟方向旋转到如图(二)中△ 位置,直线
位置,直线 与AB、CF分别相交于P、Q两点,猜想OQ、OP长度的大小关系,并证明你的猜想.
与AB、CF分别相交于P、Q两点,猜想OQ、OP长度的大小关系,并证明你的猜想.
(3)在(2)的条件下,指出当旋转角至少为多少度时,四边形PCQB为菱形(不要求证明).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com