
(本题12分)射线QN与等边△ABC的两边AB,BC分别交于点M,N,且AC∥QN,AM=MB=2cm,
QM=4cm.动点P从点Q出发,沿射线QN以每秒1cm的速度向右移动,经过t秒,以点P为圆心,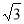 cm
cm
为半径的圆与△ABC的边相切(切点在边上),求t值(单位:秒).
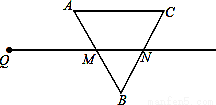
见解析
【解析】
试题分析:分为三种情况讨论:①⊙P与边AB相切;②⊙P与边AC相切;③⊙P与边BC相切.连结点P与切点,根据切线的性质可得直角三角形,又△ABC是等边三角形,所以在直角三角形中利用特殊角的三角函数值可解决问题.
试题解析:【解析】
∵△ABC是等边三角形,QN∥AC∴△BMN是等边三角形 2分
分为三种情况:
①如图1,
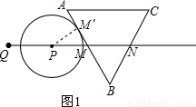
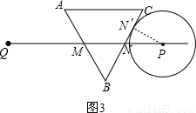
当⊙P切AB于M′时,连接PM′,则PM′=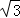 cm,∠PM′M=90°,
cm,∠PM′M=90°,
∵∠PMM′=∠BMN=60°,∴M′M=1cm,PM=2MM′=2cm,∴QP=4cm﹣2cm=2cm,即t=2; 5分
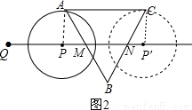
②如图2,
当⊙P于AC切于A点时,连接PA,
则∠CAP=∠APM=90°,∠PMA=∠BMN=60°,AP=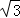 cm,∴PM=1cm,∴QP=4cm﹣1cm=3cm,
cm,∴PM=1cm,∴QP=4cm﹣1cm=3cm,
即t=3, 7分
当当⊙P于AC切于C点时,连接PC,
则∠CP′N=∠ACP′=90°,∠P′NC=∠BNM=60°,CP′=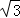 cm,
cm,
∴P′N=1cm,∴QP=4cm+2cm+1cm=7cm,
即当3≤t≤7时,⊙P和AC边相切; 9分
③如图3,
当⊙P切BC于N′时,连接PN′
则PN′=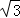 cm,∠PM\N′N=90°,
cm,∠PM\N′N=90°,
∵∠PNN′=∠BNM=60°,∴N′N=1cm,PN=2NN′=2cm,∴QP=4cm+2cm+2cm=8cm,即t=8;
综上所述:t=2或3≤t≤7或t=8. 12分
考点:1. 等边三角形的性质;2.切线的性质;3.直角三角形的性质;4.特殊角的三角函数值.


科目:初中数学 来源:2014-2015学年安徽濉溪城关中心学校八年级上学期第三次月考数学卷(解析版) 题型:选择题
能说明△ABC≌△DEF的条件是( )
A.AB=DE,AC=DF,∠C=∠F
B.AC=EF,∠A=∠D,∠B=∠E
C.AB=DE,BC=EF,∠A=∠D
D.BC=EF,AB=DE,∠B=∠E
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省盐城市阜宁县九年级上学期期中学情调研数学试卷(解析版) 题型:解答题
(本题10分)如图,AB为⊙O的直径,EF切⊙O于点D,过点B作BH⊥EF于点H,交⊙O于点C,连接BD.

(1)求证:BD平分∠ABH;
(2)如果AB=12,BC=8,求圆心O到BC的距离.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省盐城市阜宁县九年级上学期期中学情调研数学试卷(解析版) 题型:填空题
如图,⊙O的内接四边形ABCD中,∠BCD=138°,则∠BOD的度数是 .
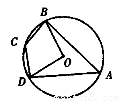
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省兴化顾庄等三校九年级上学期12月月考数学试卷(解析版) 题型:解答题
如图,Rt△ABC中,∠ABC=90°,以AB为直径作半圆⊙O交AC与点D,点E为BC的中点,连接DE.

(1)求证:DE是半圆⊙O的切线.
(2)若∠BAC=30°,DE=2,求AD的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com