
(本题10分)如图,AB为⊙O的直径,EF切⊙O于点D,过点B作BH⊥EF于点H,交⊙O于点C,连接BD.

(1)求证:BD平分∠ABH;
(2)如果AB=12,BC=8,求圆心O到BC的距离.
见解析
【解析】
试题分析:(1)连接OD,根据EF切⊙O于点D,可得OD⊥EF,又BH⊥EF,所以OD∥BH,然后证明∠ODB=∠OBD=∠DBH即可;(2)过点O作OG⊥BC于点G,由垂径定理和勾股定理可求出圆心O到BC的距离.
试题解析:(1)证明:连接OD.
∵EF是⊙O的切线,∴OD⊥EF. 2分
又∵BH⊥EF,∴OD∥BH,
∴∠ODB=∠DBH. 4分
而OD=OB,∴∠ODB=∠OBD,
∴∠OBD=∠DBH,
∴BD平分∠ABH. 5分
(2)过点O作OG⊥BC于点G,则BG=CG=4,
在Rt△OBG中,OG=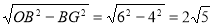 . 10分
. 10分
考点:1.切线的性质;2.圆的基本性质;3. 垂径定理;4. 勾股定理.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源:2014-2015学年安徽濉溪城关中心学校八年级上学期第三次月考数学卷(解析版) 题型:解答题
(10分)如图所示,在四边形ABCD中,AD∥BC,E为CD的中点,连接AE、BE,BE⊥AE,延长AE交BC的延长线于点F.
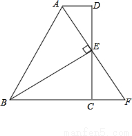
求证:(1)FC=AD;(2)AB=BC+AD.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年安徽濉溪城关中心学校八年级上学期第三次月考数学卷(解析版) 题型:选择题
在△ABC中,∠A-∠B=35°,∠C=55°,则∠B等于( )
A.50° B.55° C.45° D.40°
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省盐城市阜宁县九年级上学期期中学情调研数学试卷(解析版) 题型:解答题
(本题12分)射线QN与等边△ABC的两边AB,BC分别交于点M,N,且AC∥QN,AM=MB=2cm,
QM=4cm.动点P从点Q出发,沿射线QN以每秒1cm的速度向右移动,经过t秒,以点P为圆心,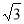 cm
cm
为半径的圆与△ABC的边相切(切点在边上),求t值(单位:秒).
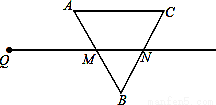
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省盐城市阜宁县九年级上学期期中学情调研数学试卷(解析版) 题型:填空题
钟表的分针长为4,从8:25到9:10,分针扫过的区域(图形)与圆锥的侧面展开图全等,
则这个圆锥底面圆的半径是 .
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省盐城市阜宁县九年级上学期期中学情调研数学试卷(解析版) 题型:填空题
若关于x的一元二次方程kx2﹣2x﹣1=0有两个不相等的实数根,则实数k的取值范围是
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省兴化顾庄等三校九年级上学期12月月考数学试卷(解析版) 题型:解答题
如图,有一路灯杆AB(底部B不能直接到达),在灯光下,小明在点D处测得自己的影长DF=3m,
沿BD方向到达点F处再测得自己的影长FG=4m.如果小明的身高为1.6m,求路灯杆AB的高度.

查看答案和解析>>
科目:初中数学 来源:2014-2015学年福建省九年级上学期第三次教学质量监测数学试卷(解析版) 题型:选择题
如图,在梯形ABCD中,AD∥BC,AD=AB,BC=BD, ∠A=140°,则∠C等于( )
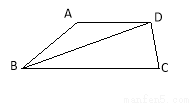
A.75° B.60° C.70° D.80°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com