
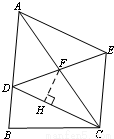
如图,在△ABC中,D为AB边上一点、F为AC的中点,过点C作CE//AB交DF的延长线于点E,连结AE.
(1)求证:四边形ADCE为平行四边形.
(2)若EF=2 ,
, ,求DC的长.
,求DC的长.

(1)证明见解析;(2)2+ .
.
【解析】
试题分析:(1)首先证明△DAF≌△ECF,则AD=CE,然后根据一组对边平行且相等的四边形是平行四边形即可证得.
(2)作FH⊥DC于点H,在Rt△DFH中利用三角函数求得FH的长,在Rt△CFH中利用勾股定理即可求解.
试题解析:(1)∵CE//AB,∴∠DAF=∠ECF.
∵F为AC的中点,∴AF=CF.
∵在△DAF和△ECF中 ,
,
∴△DAF≌△ECF(SAS).∴AD=CE.
∵CE//AB,∴ 四边形ADCE为平行四边形.
(2)如图,过点F作FH⊥DC于点H.
∵ 四边形ADCE为平行四边形.
∴ AE//DC,DF= EF=2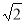 , ∴∠FDC =∠AED=45°.
, ∴∠FDC =∠AED=45°.
在Rt△DFH中,∠DHF=90°,DF=2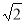 ,∠FDC=45°,
,∠FDC=45°,
∴ sin∠FDC=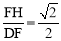 ,得FH=2,
,得FH=2,
tan∠FDC=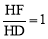 ,得DH=2.
,得DH=2.
在Rt△CFH中,∠FHC=90°,FH=2,∠FCD=30°,∴ FC=4.
由勾股定理,得HC=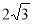 .
.
∴ DC=DH+HC=2+ .
.
考点:1.平行四边形的判定和性质;2.全等三角形的判定和性质;3.勾股定理;4.解直角三角形.


科目:初中数学 来源:2014年北京市怀柔区中考一模数学试卷(解析版) 题型:解答题
在平面直角坐标系xOy中,二次函数 的图象经过(
的图象经过(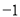 ,0)和(
,0)和( ,0)两点.
,0)两点.
(1)求此二次函数的表达式.
(2)直接写出当 <x<1时,y的取值范围.
<x<1时,y的取值范围.
(3)将一次函数 y=(1-m)x+2的图象向下平移m个单位后,与二次函数 图象交点的横坐标分别是a和b,其中a<2<b,试求m的取值范围.
图象交点的横坐标分别是a和b,其中a<2<b,试求m的取值范围.
查看答案和解析>>
科目:初中数学 来源:2014年北京市怀柔区中考一模数学试卷(解析版) 题型:选择题
在下列某品牌T恤的四个洗涤说明图案的设计中,没有运用旋转或轴对称知识的是( )
A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:初中数学 来源:2014年北京市平谷区中考一模数学试卷(解析版) 题型:解答题
(1)如图1,点E、F分别是正方形ABCD的边BC、CD上的点,∠EAF=45°,连接EF,
则EF、BE、FD之间的数量关系是:EF=BE+FD.连结BD,交AE、AF于点M、N,且MN、BM、DN满足 ,请证明这个等量关系;
,请证明这个等量关系;
(2)在△ABC中, AB=AC,点D、E分别为BC边上的两点.
①如图2,当∠BAC=60°,∠DAE=30°时,BD、DE、EC应满足的等量关系是__________________;
②如图3,当∠BAC= ,(0°<
,(0°< <90°),∠DAE=
<90°),∠DAE= 时,BD、DE、EC应满足的等量关系是____________________.【参考:
时,BD、DE、EC应满足的等量关系是____________________.【参考: 】
】

查看答案和解析>>
科目:初中数学 来源:2014届重庆一中七年级上期期末考试数学试卷(解析版) 题型:解答题
某公司要把240吨白砂糖运往某市的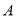 、
、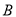 两地,用大、小两种货车共20辆,恰好能一次性装完这批白砂糖.已知这两种货车的载重量分别为15吨/辆和10吨/辆,运往
两地,用大、小两种货车共20辆,恰好能一次性装完这批白砂糖.已知这两种货车的载重量分别为15吨/辆和10吨/辆,运往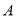 地的运费为:大车630元/辆,小车420元/辆;运往
地的运费为:大车630元/辆,小车420元/辆;运往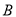 地的运费为:大车750元/辆,小车550元/辆.
地的运费为:大车750元/辆,小车550元/辆.
(1)求两种货车各用多少辆;
(2)如果安排10辆货车前往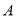 地,其中调往
地,其中调往 地的大车有
地的大车有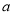 辆,其余货车前往
辆,其余货车前往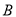 地,若设总运费为
地,若设总运费为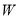 ,求W与
,求W与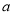 的关系式(用含有
的关系式(用含有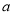 的代数式表示W).
的代数式表示W).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com