
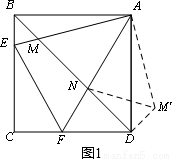
(1)如图1,点E、F分别是正方形ABCD的边BC、CD上的点,∠EAF=45°,连接EF,
则EF、BE、FD之间的数量关系是:EF=BE+FD.连结BD,交AE、AF于点M、N,且MN、BM、DN满足 ,请证明这个等量关系;
,请证明这个等量关系;
(2)在△ABC中, AB=AC,点D、E分别为BC边上的两点.
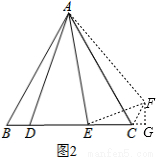
①如图2,当∠BAC=60°,∠DAE=30°时,BD、DE、EC应满足的等量关系是__________________;
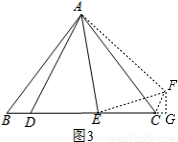
②如图3,当∠BAC= ,(0°<
,(0°< <90°),∠DAE=
<90°),∠DAE= 时,BD、DE、EC应满足的等量关系是____________________.【参考:
时,BD、DE、EC应满足的等量关系是____________________.【参考: 】
】

(1)证明见解析;(2)①DE2=BD2+BD•EC+EC2;②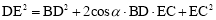 .
.
【解析】
试题分析:(1)如图1,把△ABM绕点A逆时针旋转90°得到△ADM',连接NM′.就可以得出△ABM≌△ADM′,就有∠BAM=∠DAM′,就可以得出△AMN≌△AM′N就可以得出MN=M′N,由勾股定理就可以得出结论MN2=DN2+BM2.
(2)①如图2,把△ABD绕点A逆时针旋转60°得到△ACF,连接EF.就可以得出△ABD≌△ACF,就有∠BAD=∠CAF,∠B=∠ACF,就可以得到∠DAE=∠FAE,得出△ADE≌△AFE,就有DE=FE,在△EFC中,作FG⊥EC的延长线于点G,由三角函数值就可以得出CG=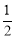 CF,GF=
CF,GF=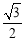 CF,在Rt△EGF中由勾股定理就可以得出结论.
CF,在Rt△EGF中由勾股定理就可以得出结论.
②如图3,把△ABD绕点A逆时针旋转a得到△ACF,连接EF.就可以得出△ABD≌△ACF,就有∠BAD=∠CAF,∠B=∠ACF,就可以得到∠DAE=∠FAE,得出△ADE≌△AFE,就有DE=FE,在△EFC中,作FG⊥EC的延长线于点G,由三角函数值就可以得出CG=cosa•CF,GF=sina•CF,在Rt△EGF中由勾股定理就可以得出结论.
试题解析:(1)如图1,在正方形ABCD中,AB=AD,∠BAD=90°,∴∠ABM=∠ADN=45°.
把△ABM绕点A逆时针旋转90°得到△ADM'.连结NM'.
∴△ABM≌△ADM′.∴DM'=BM,AM'=AM,∠ADM'=∠ABM=45°,∠DAM'=∠BAM.
∴∠ADB+∠ADM′=45°+45°=90°,即∠NDM′=90°.
∵∠EAF=45°,∴∠BAM+∠DAN=45°.∴∠DAM′+∠DAF=45°,即∠M′AN=45°.∴∠M'AN=∠MAN.
在△AMN和△AM′N中,AM=AM′,∠MAN=∠M′AN,AN=AN,
∴△AMN≌△AM′N(SAS).∴M'N=MN.
∵∠NDM′=90°,∴M'N2=DN2+DM'2,
∴MN2=DN2+BM2.
(2)①BD、DE、EC关系式为:DE2=BD2+BD•EC+EC2.理由如下:
如图2,把△ABD绕点A逆时针旋转60°得到△ACF,连接EF,作FG⊥EC的延长线于点G.
∴△ABD≌△ACF,∠FGC=90°.∴AD=AF,BD=CF,∠BAD=∠CAF,∠B=ACF.
∵∠BAC=60°,AB=AC,∴△ABC是等边三角形.∴∠B=∠ACB=60°.∴∠ACF=60°.
∴∠ACF+∠ACB=60°+60°=120°,即∠ECF=120°.∴∠FCG=60°.∴∠CFG=30°.
∴CG=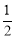 CF.
CF.
在Rt△CFG中,由勾股定理,得FG=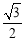 CF.
CF.
∵∠DAE=30°,∴∠BAD+∠EAC=30°.∴∠CAF+∠EAC=30°,即∠EAF=30°.∴∠DAE=∠FAE.
在△ADE和△AFE中,AD=AE,∠DAE=∠FAE,∠AE=AE,
∴△ADE≌△AFE(SAS).∴DE=EF.
在Rt△EGF中,由勾股定理,得EF2=EG2+FG2,
∴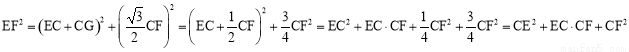 .
.
②BD、DE、EC等量关系是: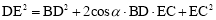 .理由如下:
.理由如下:
把△ABD绕点A逆时针旋转a得到△ACF,连接EF.作FG⊥EC的延长线于点G.
∴△ABD≌△ACF,∠FGC=90°.
∴AD=AF,BD=CF,∠BAD=∠CAF,∠B=ACF.
∵AB=AC,∴∠B=∠ACB.
∵∠B+∠ACB+∠BAC=180°,∠ACB+∠ACF+∠FCG=180°,∴∠BAC=∠FCG=α.
∴∠ACF=60°.
∴CG=cosα•CF,FG=sinα•CF.
∵∠DAE=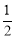 α,∴∠BAD+∠CAE=
α,∴∠BAD+∠CAE=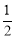 α.
α.
∴∠CAF+∠CAE=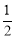 α,即∠EAF=
α,即∠EAF=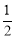 α.
α.
∴∠DAE=∠FAE.
在△ADE和△AFE中,AD=AE,∠DAE=∠FAE,∠AE=AE,
∴△ADE≌△AFE(SAS).∴DE=EF.
在Rt△EGF中,由勾股定理,得EF2=EG2+FG2,
∴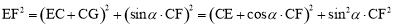
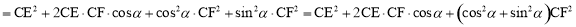
∵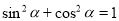 ,
,
∴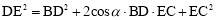 .
.
考点:1.正方形的性质;2.等边三角形的性质;3.等腰三角形的性质;4.旋转的性质;5.全等三角形的判定和性质;6.勾股定理;7.三角函数值的运用.


科目:初中数学 来源:2014年北京市房山区中考二模数学试卷(解析版) 题型:解答题
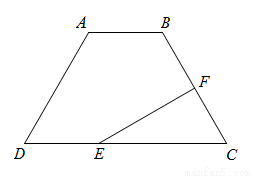
已知:如图,梯形ABCD中,AD=BC,F为BC的中点,AB=2,∠A=120°,过点F作EF⊥BC交DC于点E,且EF= 3 ,求DC的长.
查看答案和解析>>
科目:初中数学 来源:2014年北京市房山区中考一模数学试卷(解析版) 题型:选择题
某班共有学生31名,其中男生11名.老师随机请一名同学回答问题,则男生被选中的概率是( )
A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:初中数学 来源:2014年北京市怀柔区中考一模数学试卷(解析版) 题型:填空题
请写出一个在各自象限内,y的值随着x值的增大而减小的反比例函数的表达式_____________.
查看答案和解析>>
科目:初中数学 来源:2014年北京市怀柔区中考一模数学试卷(解析版) 题型:选择题
掷一枚质地均匀的正方体骰子,骰子的六个面上分别刻有1 到6的点数,掷得面朝上的点数小于3的概率为( )
A. B.
B.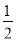 C.
C. D.
D.
查看答案和解析>>
科目:初中数学 来源:2014年北京市平谷区中考一模数学试卷(解析版) 题型:解答题
如图,在△ABC中,D为AB边上一点、F为AC的中点,过点C作CE//AB交DF的延长线于点E,连结AE.
(1)求证:四边形ADCE为平行四边形.
(2)若EF=2 ,
, ,求DC的长.
,求DC的长.

查看答案和解析>>
科目:初中数学 来源:2014年北京市平谷区中考一模数学试卷(解析版) 题型:填空题
如图,P1、P2、P3…Pn(n为正整数)分别是反比例函数 在第一象限图象上的点,A1、A2、A3…An分别为x轴上的点,且△P1OA1、△P2A1A2、△P3A2A3…△PnAn-1An均为等边三角形.若点A1的坐标为(2,0),则点A2的坐标为__________________,点An的坐标为__________________.
在第一象限图象上的点,A1、A2、A3…An分别为x轴上的点,且△P1OA1、△P2A1A2、△P3A2A3…△PnAn-1An均为等边三角形.若点A1的坐标为(2,0),则点A2的坐标为__________________,点An的坐标为__________________.

查看答案和解析>>
科目:初中数学 来源:2014年北京市密云县中考一模数学试卷(解析版) 题型:解答题
某同学在学习了统计知识后,就下表所列的5种用牙不良习惯对全班每一个同学进行了问卷调查(每个被调查的同学必须选择而且只能在5种用牙不良习惯中选择一项),调查结果如下统计图所示.根据以上统计图提供的信息,回答下列问题:
种类 | A | B | C | D | E |
不良习惯 | 睡前吃水果喝牛奶 | 用牙开瓶盖 | 常喝饮料嚼冰 | 常吃生冷零食 | 磨牙 |
(1)这个班有多少名学生?
(2)这个班中有C类用牙不良习惯的学生多少人?占全班人数的百分比是多少?
(3)请补全条形统计图;
(4)根据调查结果,估计这个年级850名学生中有B类用牙不良习惯的学生多少人?

查看答案和解析>>
科目:初中数学 来源:2014年北京市东城区中考一模数学试卷(解析版) 题型:选择题
有五张形状、大小、质地都相同的卡片,上面分别画有下列图形:①正方形;②正三角形;③平行四边形;④等腰梯形;⑤圆.将卡片背面朝上洗匀,从中随机抽取一张,正面图形既是轴对称图形,又是中心对称图形的概率是( )
A. B.
B. C.
C. D.
D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com