
【题目】抛物线![]() 上部分点的横坐标
上部分点的横坐标![]() ,纵坐标
,纵坐标![]() 的对应值如下表:
的对应值如下表:
|
| -3 | -2 | -1 | 0 | 1 |
|
|
| 0 | 4 | 3 | 0 |
|
(1)把表格填写完整;
(2)根据上表填空:
①抛物线与![]() 轴的交点坐标是________和__________;
轴的交点坐标是________和__________;
②在对称轴右侧,![]() 随
随![]() 增大而_______________;
增大而_______________;
③当![]() 时,则
时,则![]() 的取值范围是_________________;
的取值范围是_________________;
(3)请直接写出抛物线![]() 的解析式.
的解析式.
【答案】(1)3;(2)①抛物线与![]() 轴的交点坐标是
轴的交点坐标是![]() 和
和![]() ;②
;②![]() 随
随![]() 增大而减小;③
增大而减小;③![]() 的取值范围是
的取值范围是![]() ;(3)
;(3)![]() .
.
【解析】
(1)利用表中对应值的特征和抛物线的对称性得到抛物线的对称轴为直线x=-1,则x=0和x=-2时,y的值相等,都为3;
(2)①利用表中y=0时x的值可得到抛物线与x轴的交点坐标;
②设交点式y=a(x+3)(x-1),再把(0,3)代入求出a得到抛物线解析式为y=-x2-2x+3,则可判断抛物线的顶点坐标为(-1,4),抛物线开口向下,然后根据二次函数的性质解决问题;③由于x=-2时,y=3;当x=2时,y=-5,结合二次函数的性质可确定y的取值范围;
(3)由(2)得抛物线解析式.
解:(1)∵x=-3,y=0;x=1,y=0,
∴抛物线的对称轴为直线x=-1,
∴x=0和x=-2时,y=3;
故答案是:3;
(2)①∵x=-3,y=0;x=1,y=0,
∴抛物线与x轴的交点坐标是(-3,0)和(1,0);
故答案是:(-3,0)和(1,0);
②设抛物线解析式为y=a(x+3)(x-1),
把(0,3)代入得3=-3a,解得a=-1,
∴抛物线解析式为y=-(x+3)(x-1),即y=-x2-2x+3,
抛物线的顶点坐标为(-1,4),抛物线开口向下,
∴在对称轴右侧,y随x增大而减小;
故答案是:减小;
③当x=-2时,y=3;当x=2时,y=-4-4+3=-5,当x=-1,y有最大值为4,
∴当-2<x<2时,则y的取值范围是-5<y≤4.
故答案是:-5<y≤4;
(3)由(2)得抛物线解析式为y=-x2-2x+3,
故答案是:y=-x2-2x+3.


科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠A=90°,AB=20cm,AC=15cm,在这个直角三角形内有一个内接正方形,正方形的一边FG在BC上,另两个顶点E、H分别在边AB、AC上.
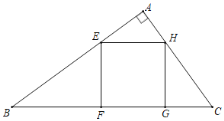
(1)求BC边上的高;
(2)求正方形EFGH的边长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,将一块含有45°角的直角三角板如图放置,直角顶点C的坐标为(1,0),顶点A的坐标为(0,2),顶点B恰好落在第一象限的双曲线上,现将直角三角板沿x轴正方向平移,当顶点A恰好落在该双曲线上时停止运动,则此时点C的对应点C′的坐标为( )
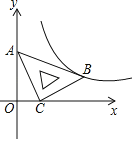
A.(![]() ,0)B.(2,0)C.(
,0)B.(2,0)C.(![]() ,0)D.(3,0)
,0)D.(3,0)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】游泳是一项深受青少年喜爱的体育运动,某中学为了加强学生的游泳安全意识,组织学生观看了纪实片“孩子,请不要私自下水”,并于观看后在本校的![]() 名学生中作了抽样调查.制作了下面两个不完整的统计图.请根据这两个统计图回答以下问题:
名学生中作了抽样调查.制作了下面两个不完整的统计图.请根据这两个统计图回答以下问题:

(I)这次抽样调查中,共调查了 名学生;
(2)补全两个统计图;
(3)根据抽样调查的结果,估算该校![]() 名学生中大约有多少人“结伴时会下河学游泳”?
名学生中大约有多少人“结伴时会下河学游泳”?
查看答案和解析>>
科目:初中数学 来源: 题型:
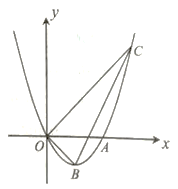
【题目】如图,抛物线![]() 过原点,且与
过原点,且与![]() 轴交于点
轴交于点![]() .
.
(1)求抛物线的解析式及顶点![]() 的坐标;
的坐标;
(2)已知![]() 为抛物线上一点,连接
为抛物线上一点,连接![]() ,
,![]() ,
,![]() ,求
,求![]() 的值;
的值;
(3)在第一象限的抛物线上是否存在一点![]() ,过点
,过点![]() 作
作![]() 轴于点
轴于点![]() ,使以
,使以![]() ,
,![]() ,
,![]() 三点为顶点的三角形与
三点为顶点的三角形与![]() 相似,若存在,求出满足条件的点
相似,若存在,求出满足条件的点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
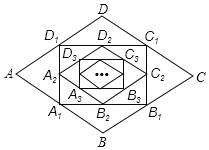
【题目】如图,在菱形ABCD中,边长为1,∠A=60,顺次连接菱形ABCD各边中点,可得四边形A1B1C1D1;顺次连结四边形A1B1C1D1各边中点,可得四边形A2B2C2D2;顺次连结四边形A2B2C2D2各边中点,可得四边形A3B3C3D3;按此规律继续下去,…,则四边形A2019B2019C2019D2019的面积是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
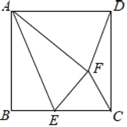
【题目】如图,正方形ABCD的边长为6,点E边BC上,连接AE,将△ABE沿着AE翻折到△AEF,连接CF、DF,若△CDF为等腰三角形,则△CDF的面积为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,是二次函数y=ax2+bx+c图象的一部分,其对称轴是x=﹣1,且过点(﹣3,0),下列说法:①abc<0;②2a﹣b=0;③若(﹣5,y1),(3,y2)是抛物线上两点,则y1=y2;④4a+2b+c<0,其中说法正确的( )
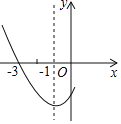
A.①②B.①②③C.①②④D.②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为积极响应党和国家精准扶贫战略计划,某公司在农村租用了 720亩闲置土地种植了乔 木型、小乔木型和灌木型三种茶树. 为达到最佳种植收益,要求种植乔木型茶树的面积是小乔木型茶树面积的2倍,灌木型茶树的面积不得超过乔木型茶树面积的![]() 倍,但种植乔木型茶树的面积不得超过270亩. 到茶叶采摘季节时,该公司聘请当地农民进行采摘,每人每天可以采摘0.4亩乔木型茶叶,或者采摘0.5亩小乔木型茶叶,或者采摘0.6亩灌木型茶叶. 若该公司聘请一批农民恰好20天能采摘完所有茶叶,则种植乔木型茶树的面积是________亩.
倍,但种植乔木型茶树的面积不得超过270亩. 到茶叶采摘季节时,该公司聘请当地农民进行采摘,每人每天可以采摘0.4亩乔木型茶叶,或者采摘0.5亩小乔木型茶叶,或者采摘0.6亩灌木型茶叶. 若该公司聘请一批农民恰好20天能采摘完所有茶叶,则种植乔木型茶树的面积是________亩.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com