
ЁОЬтФПЁПЮЊЛ§МЋЯьгІЕГКЭЙњМвОЋзМЗіЦЖеНТдМЦЛЎЃЌФГЙЋЫОдкХЉДхзтгУСЫ 720ФЖЯажУЭСЕижжжВСЫЧЧ ФОаЭЁЂаЁЧЧФОаЭКЭЙрФОаЭШ§жжВшЪї. ЮЊДяЕНзюМбжжжВЪевцЃЌвЊЧѓжжжВЧЧФОаЭВшЪїЕФУцЛ§ЪЧаЁЧЧФОаЭВшЪїУцЛ§ЕФ2БЖЃЌЙрФОаЭВшЪїЕФУцЛ§ВЛЕУГЌЙ§ЧЧФОаЭВшЪїУцЛ§ЕФ![]() БЖЃЌЕЋжжжВЧЧФОаЭВшЪїЕФУцЛ§ВЛЕУГЌЙ§270ФЖ. ЕНВшвЖВЩеЊМОНкЪБЃЌИУЙЋЫОЦИЧыЕБЕиХЉУёНјааВЩеЊЃЌУПШЫУПЬьПЩвдВЩеЊ0.4ФЖЧЧФОаЭВшвЖЃЌЛђепВЩеЊ0.5ФЖаЁЧЧФОаЭВшвЖЃЌЛђепВЩеЊ0.6ФЖЙрФОаЭВшвЖ. ШєИУЙЋЫОЦИЧывЛХњХЉУёЧЁКУ20ЬьФмВЩеЊЭъЫљгаВшвЖЃЌдђжжжВЧЧФОаЭВшЪїЕФУцЛ§ЪЧ________ФЖ.
БЖЃЌЕЋжжжВЧЧФОаЭВшЪїЕФУцЛ§ВЛЕУГЌЙ§270ФЖ. ЕНВшвЖВЩеЊМОНкЪБЃЌИУЙЋЫОЦИЧыЕБЕиХЉУёНјааВЩеЊЃЌУПШЫУПЬьПЩвдВЩеЊ0.4ФЖЧЧФОаЭВшвЖЃЌЛђепВЩеЊ0.5ФЖаЁЧЧФОаЭВшвЖЃЌЛђепВЩеЊ0.6ФЖЙрФОаЭВшвЖ. ШєИУЙЋЫОЦИЧывЛХњХЉУёЧЁКУ20ЬьФмВЩеЊЭъЫљгаВшвЖЃЌдђжжжВЧЧФОаЭВшЪїЕФУцЛ§ЪЧ________ФЖ.
ЁОД№АИЁП260.
ЁОНтЮіЁП
ЩшжжжВаЁЧЧФОаЭВшЪїxФЖЃЌИљОнжжжВЧЧФОаЭВшЪїЕФУцЛ§ЪЧаЁЧЧФОаЭВшЪїУцЛ§ЕФ2БЖЃЌЙрФОаЭВшЪїЕФУцЛ§ВЛЕУГЌЙ§ЧЧФОаЭВшЪїУцЛ§ЕФ![]() БЖСаГіВЛЕШЪНЃЌДгЖјЧѓГіxЕФШЁжЕЗЖЮЇЃЛдйЫљЩшЙЋЫОЦИЧыХЉУёmШЫЃЌВЩеЊЧЧФОаЭВшвЖaЬьЃЌВЩеЊаЁЧЧФОаЭВшвЖbЬьЃЌВЩеЊЙрФОаЭВшвЖЃЈ20-a-bЃЉЬьЃЌСаГіЯргІЕШЪНЃЌЯћШЅaКЭbЕУГіmгыxЙиЯЕЃЌдйДњШыЧАУцЫљЧѓЕФxЕФШЁжЕЗЖЮЇЃЌЧѓГіmЕФШЁжЕЗЖЮЇЃЌРћгУmЮЊећЪ§ЕФЬиеїзюжеЧѓГіmЕФжЕЃЌдйЧѓГіxЕФжЕ.
БЖСаГіВЛЕШЪНЃЌДгЖјЧѓГіxЕФШЁжЕЗЖЮЇЃЛдйЫљЩшЙЋЫОЦИЧыХЉУёmШЫЃЌВЩеЊЧЧФОаЭВшвЖaЬьЃЌВЩеЊаЁЧЧФОаЭВшвЖbЬьЃЌВЩеЊЙрФОаЭВшвЖЃЈ20-a-bЃЉЬьЃЌСаГіЯргІЕШЪНЃЌЯћШЅaКЭbЕУГіmгыxЙиЯЕЃЌдйДњШыЧАУцЫљЧѓЕФxЕФШЁжЕЗЖЮЇЃЌЧѓГіmЕФШЁжЕЗЖЮЇЃЌРћгУmЮЊећЪ§ЕФЬиеїзюжеЧѓГіmЕФжЕЃЌдйЧѓГіxЕФжЕ.
НтЃКЩшжжжВаЁЧЧФОаЭВшЪїxФЖЃЌдђЧЧФОаЭВшЪї2xФЖЁЂКЭЙрФОаЭВшЪїЃЈ720-3xЃЉФЖЃЛЙЋЫОЦИЧыХЉУёmШЫЃЌВЩеЊЧЧФОаЭВшвЖaЬьЃЌВЩеЊаЁЧЧФОаЭВшвЖbЬьЃЌВЩеЊЙрФОаЭВшвЖЃЈ20-a-bЃЉЬьЃЌвРЬтвтЕУЃК
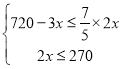
НтЕУ![]()
ЁпУПШЫУПЬьПЩвдВЩеЊ0.4ФЖЧЧФОаЭВшвЖЃЌЛђепВЩеЊ0.5ФЖаЁЧЧФОаЭВшвЖЃЌЛђепВЩеЊ0.6ФЖЙрФОаЭВшвЖЃЌ
Ёр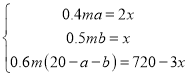
Ёр![]()
Ёр![]()
Ёр![]()
ЁпmЮЊШЫЪ§ЃЌгІЮЊећЪ§ЃЌ
Ёрm=73
Ёр![]() ЃН130
ЃН130
Ёр2x=260
ЁржжжВЧЧФОаЭВшЪїЕФУцЛ§ЪЧ260ФЖ.
ЙЪД№АИЮЊ260.


 дФЖСПьГЕЯЕСаД№АИ
дФЖСПьГЕЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПХзЮяЯп![]() ЩЯВПЗжЕуЕФКсзјБъ
ЩЯВПЗжЕуЕФКсзјБъ![]() ЃЌзнзјБъ
ЃЌзнзјБъ![]() ЕФЖдгІжЕШчЯТБэЃК
ЕФЖдгІжЕШчЯТБэЃК
|
| -3 | -2 | -1 | 0 | 1 |
|
|
| 0 | 4 | 3 | 0 |
|
(1)АбБэИёЬюаДЭъећЃЛ
(2)ИљОнЩЯБэЬюПеЃК
ЂйХзЮяЯпгы![]() жсЕФНЛЕузјБъЪЧ________КЭ__________ЃЛ
жсЕФНЛЕузјБъЪЧ________КЭ__________ЃЛ
ЂкдкЖдГЦжсгвВрЃЌ![]() Ыц
Ыц![]() діДѓЖј_______________ЃЛ
діДѓЖј_______________ЃЛ
ЂлЕБ![]() ЪБЃЌдђ
ЪБЃЌдђ![]() ЕФШЁжЕЗЖЮЇЪЧ_________________ЃЛ
ЕФШЁжЕЗЖЮЇЪЧ_________________ЃЛ
(3)ЧыжБНгаДГіХзЮяЯп![]() ЕФНтЮіЪНЃЎ
ЕФНтЮіЪНЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
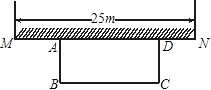
ЁОЬтФПЁПШчЭМЃЌФГжабЇзМБИдкаЃдАРяРћгУЮЇЧНЕФвЛЖЮЃЌдйЦіШ§УцЧНЃЌЮЇГЩвЛИіОиаЮЛЈдАABCDЃЈЮЇЧНMNзюГЄПЩРћгУ25mЃЉЃЌЯждквбБИзуПЩвдЦі50mГЄЕФЧНЕФВФСЯЃЌЪдЩшМЦвЛжжЦіЗЈЃЌЪЙОиаЮЛЈдАЕФУцЛ§ЮЊ300m2ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊЖўДЮКЏЪ§ЕФЭМЯѓЕФЖЅЕузјБъЮЊ![]() ЃЌжБЯп
ЃЌжБЯп![]() гыИУЖўДЮКЏЪ§ЕФЭМЯѓНЛгк
гыИУЖўДЮКЏЪ§ЕФЭМЯѓНЛгк![]() ЃЌ
ЃЌ![]() СНЕуЃЌЦфжаЕу
СНЕуЃЌЦфжаЕу![]() ЕФзјБъЮЊ
ЕФзјБъЮЊ![]() ЃЌЕу
ЃЌЕу![]() дк
дк![]() жсЩЯЃЎ
жсЩЯЃЎ![]() ЪЧ
ЪЧ![]() жсЩЯЕФвЛИіЖЏЕуЃЌЙ§Еу
жсЩЯЕФвЛИіЖЏЕуЃЌЙ§Еу![]() зї
зї![]() жсЕФДЙЯпЗжБ№гыжБЯп
жсЕФДЙЯпЗжБ№гыжБЯп![]() КЭЖўДЮКЏЪ§ЕФЭМЯѓНЛгк
КЭЖўДЮКЏЪ§ЕФЭМЯѓНЛгк![]() ЃЌ
ЃЌ![]() СНЕуЃЎ
СНЕуЃЎ
ЃЈ1ЃЉЧѓ![]() ЕФжЕМАетИіЖўДЮКЏЪ§ЕФНтЮіЪНЃЛ
ЕФжЕМАетИіЖўДЮКЏЪ§ЕФНтЮіЪНЃЛ
ЃЈ2ЃЉШєЕу![]() ЕФКсзјБъ
ЕФКсзјБъ![]() ЃЌЧѓ
ЃЌЧѓ![]() ЕФУцЛ§ЃЛ
ЕФУцЛ§ЃЛ
ЃЈ3ЃЉЕБ![]() ЪБЃЌЧѓЯпЖЮ
ЪБЃЌЧѓЯпЖЮ![]() ЕФзюДѓжЕЃЛ
ЕФзюДѓжЕЃЛ
ЃЈ4ЃЉШєжБЯп![]() гыЖўДЮКЏЪ§ЭМЯѓЕФЖдГЦжсНЛЕуЮЊ
гыЖўДЮКЏЪ§ЭМЯѓЕФЖдГЦжсНЛЕуЮЊ![]() ЃЌЮЪЪЧЗёДцдкЕу
ЃЌЮЪЪЧЗёДцдкЕу![]() ЃЌЪЙвд
ЃЌЪЙвд![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЮЊЖЅЕуЕФЫФБпаЮЪЧЦНааЫФБпаЮЃПШєДцдкЃЌЧыЧѓГіДЫЪБЕу
ЮЊЖЅЕуЕФЫФБпаЮЪЧЦНааЫФБпаЮЃПШєДцдкЃЌЧыЧѓГіДЫЪБЕу![]() ЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЁЖОХеТЫуЪѕЁЗМЧдиЁАНёгавиЗНВЛжЊДѓаЁЃЌИїжаПЊУХЃЎГіББУХШ§ЪЎВНгаФОЃЌГіЮїУХЦпАйЮхЪЎВНМћФОЃЎЮЪвиЗНгаМИКЮЃПЁБвтЫМЪЧЃКШчЭМЃЌЕуMЁЂЕуNЗжБ№ЪЧе§ЗНаЮABCDЕФБпADЁЂABЕФжаЕуЃЌMEЁЭADЃЌNFЁЭABЃЌEFЙ§ЕуAЃЌЧвME=30ВНЃЌNF=750ВНЃЌдђе§ЗНаЮЕФБпГЄЮЊЃЈЁЁЁЁЃЉ
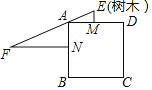
A. 150ВНB. 200ВНC. 250ВНD. 300ВН
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
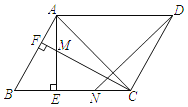
ЁОЬтФПЁПШчЭМЃЌдкABCDжаЃЌЁЯACBЃН45ЁуЃЌAEЁЭBCгкЕуEЃЌЙ§ЕуCзїCFЁЭABгкЕуFЃЌНЛAEгкЕуMЃЎЕуNдкБпBCЩЯЃЌЧвAMЃНCNЃЌСЌНсDNЃЎ
ЃЈ1ЃЉШєABЃН![]() ЃЌACЃН4ЃЌЧѓBCЕФГЄЃЛ
ЃЌACЃН4ЃЌЧѓBCЕФГЄЃЛ
ЃЈ2ЃЉЧѓжЄЃКAD+AMЃН![]() DNЃЎ
DNЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
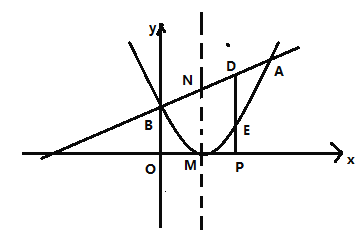
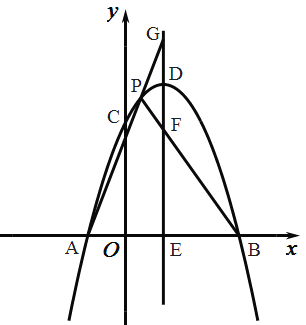
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌХзЮяЯпy=ax2+bx+cНЛxжсгкAЁЂBСНЕуЃЌOA=1ЃЌOB=3ЃЌХзЮяЯпЕФЖЅЕузјБъЮЊDЃЈ1ЃЌ4ЃЉ.
ЃЈ1ЃЉЧѓAЁЂBСНЕуЕФзјБъЃЛ
ЃЈ2ЃЉЧѓХзЮяЯпЕФБэДяЪНЃЛ
ЃЈ3ЃЉЙ§ЕуDзіжБЯпDE//yжсЃЌНЛxжсгкЕуE,ЕуPЪЧХзЮяЯпЩЯAЁЂDСНЕуМфЕФвЛИіЖЏЕуЃЈЕуPВЛгкAЁЂDСНЕужиКЯЃЉЃЌPAЁЂPBгыжБЯпDEЗжБ№НЛгкЕуGЁЂFЃЌЕБЕуPдЫЖЏЪБЃЌEF+EGЕФжЕЪЧЗёБфЛЏЃЌШчВЛБфЃЌЪдЧѓГіИУжЕЃЛШєБфЛЏЃЌЧыЫЕУїРэгЩЁЃ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌPЪЧХзЮяЯпy=Љx2+x+2дкЕквЛЯѓЯоЩЯЕФЕуЃЌЙ§ЕуPЗжБ№ЯђxжсКЭyжсв§ДЙЯпЃЌДЙзуЗжБ№ЮЊAЃЌBЃЌдђЫФБпаЮOAPBжмГЄЕФзюДѓжЕЮЊ_____ЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
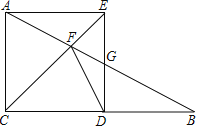
ЁОЬтФПЁПдкRtЁїABCжаЃЌЁЯACB=90ЁуЃЌAC=12ЃЎЕуDдкжБЯпCBЩЯЃЌвдCAЃЌCDЮЊБпзїОиаЮACDEЃЌжБЯпABгыжБЯпCEЃЌDEЕФНЛЕуЗжБ№ЮЊFЃЌGЃЌ
ЃЈ1ЃЉШчЭМЃЌЕуDдкЯпЖЮCBЩЯЃЌЫФБпаЮACDEЪЧе§ЗНаЮЃЎ
ЂйШєЕуGЮЊDEЕФжаЕуЃЌЧѓFGЕФГЄЃЎ
ЂкШєDG=GFЃЌЧѓBCЕФГЄЃЎ
ЃЈ2ЃЉвбжЊBC=9ЃЌЪЧЗёДцдкЕуDЃЌЪЙЕУЁїDFGЪЧЕШбќШ§НЧаЮЃПШєДцдкЃЌЧѓИУШ§НЧаЮЕФбќГЄЃЛШєВЛДцдкЃЌЪдЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com