【题目】如图，是二次函数y＝ax2+bx+c图象的一部分，其对称轴是x＝﹣1，且过点(﹣3，0)，下列说法：①abc＜0；②2a﹣b＝0；③若(﹣5，y1)，(3，y2)是抛物线上两点，则y1＝y2；④4a+2b+c＜0，其中说法正确的（ ）
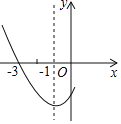
A.①②B.①②③C.①②④D.②③④
阅读快车系列答案科目：初中数学 来源： 题型：
【题目】只有1和它本身两个因数且大于1的正整数叫做素数．我国数学家陈景润在哥德巴赫猜想的研究中取得了世界领先的成果，哥德巴赫猜想是：每个大于2的偶数都可以表示为两个素数的和，如16=3+ 13．
（1）若从7， 11， 19， 23中随机抽取1个素数，则抽到的素数是7的概率是_______；
（2）若从7， 11， 19， 23中随机抽取1个素数，再从余下的3个数字中随机抽取1个素数，用面树状图或列表的方法求抽到的两个素数之和大于等于30的概率，
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】抛物线
上部分点的横坐标
，纵坐标
的对应值如下表：
|
| -3 | -2 | -1 | 0 | 1 |
|
|
| 0 | 4 | 3 | 0 |
|
(1)把表格填写完整；
(2)根据上表填空：
①抛物线与轴的交点坐标是________和__________；
②在对称轴右侧，随增大而_______________；
③当
时，则
的取值范围是_________________；
(3)请直接写出抛物线的解析式．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，△ABC是一块锐角三角形材料，高线AH长8 cm，底边BC长10 cm，要把它加工成一个矩形零件，使矩形DEFG的一边EF在BC上，其余两个顶点D，G分别在AB，AC上，则四边形DEFG的最大面积为( )
A. 40 cm2 B. 20 cm2
C. 25 cm2 D. 10 cm2
查看答案和解析>>
科目：初中数学 来源： 题型：
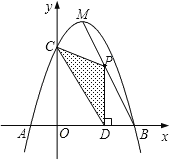
【题目】如图，抛物线y＝﹣x2+bx+c与x轴相交于A、B两点，与y轴相交于点C，且点B与点C的坐标分别为B(3，0)，C(0，3)，点M是抛物线的顶点．
（1）求二次函数的关系式；
（2）点P为线段MB上一个动点，过点P作PD⊥x轴于点D．若OD＝m，△PCD的面积为S，
①求S与m的函数关系式，写出自变量m的取值范围．
②当S取得最值时，求点P的坐标；
（3）在MB上是否存在点P，使△PCD为直角三角形？如果存在，请直接写出点P的坐标；如果不存在，请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
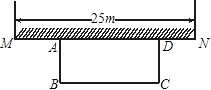
【题目】如图，某中学准备在校园里利用围墙的一段，再砌三面墙，围成一个矩形花园ABCD（围墙MN最长可利用25m），现在已备足可以砌50m长的墙的材料，试设计一种砌法，使矩形花园的面积为300m2．
查看答案和解析>>
科目：初中数学 来源： 题型：
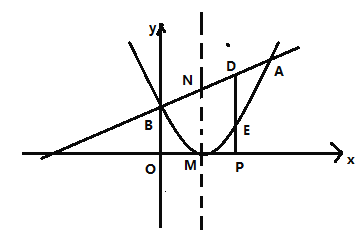
【题目】如图，已知二次函数的图象的顶点坐标为
，直线
与该二次函数的图象交于
，
两点，其中点的坐标为
，点在
轴上．
是
轴上的一个动点，过点
作轴的垂线分别与直线
和二次函数的图象交于
，
两点．
（1）求
的值及这个二次函数的解析式；
（2）若点的横坐标
，求
的面积；
（3）当
时，求线段
的最大值；
（4）若直线与二次函数图象的对称轴交点为
，问是否存在点，使以
，，，为顶点的四边形是平行四边形？若存在，请求出此时点的坐标；若不存在，请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，P是抛物线y=﹣x2+x+2在第一象限上的点，过点P分别向x轴和y轴引垂线，垂足分别为A，B，则四边形OAPB周长的最大值为_____．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
