
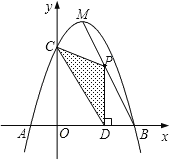
【题目】如图,抛物线y=﹣x2+bx+c与x轴相交于A、B两点,与y轴相交于点C,且点B与点C的坐标分别为B(3,0),C(0,3),点M是抛物线的顶点.
(1)求二次函数的关系式;
(2)点P为线段MB上一个动点,过点P作PD⊥x轴于点D.若OD=m,△PCD的面积为S,
①求S与m的函数关系式,写出自变量m的取值范围.
②当S取得最值时,求点P的坐标;
(3)在MB上是否存在点P,使△PCD为直角三角形?如果存在,请直接写出点P的坐标;如果不存在,请说明理由.
【答案】(1)y=﹣x2+2x+3;(2)①S=﹣m2+3m,1≤m≤3;②P(![]() ,3);(3)存在,点P的坐标为(
,3);(3)存在,点P的坐标为(![]() ,3)或(﹣3+3
,3)或(﹣3+3![]() ,12﹣6
,12﹣6![]() ).
).
【解析】
(1)将点B,C的坐标代入![]() 即可;
即可;
(2)①求出顶点坐标,直线MB的解析式,由PD⊥x轴且![]() 知P(m,﹣2m+6),即可用含m的代数式表示出S;
知P(m,﹣2m+6),即可用含m的代数式表示出S;
②在①的情况下,将S与m的关系式化为顶点式,由二次函数的图象及性质即可写出点P的坐标;
(3)分情况讨论,如图2﹣1,当![]() 时,推出
时,推出![]() ,则点P纵坐标为3,即可写出点P坐标;如图2﹣2,当
,则点P纵坐标为3,即可写出点P坐标;如图2﹣2,当![]() 时,证
时,证![]() ,由锐角三角函数可求出m的值,即可写出点P坐标;当
,由锐角三角函数可求出m的值,即可写出点P坐标;当![]() 时,不存在点P.
时,不存在点P.
(1)将点B(3,0),C(0,3)代入![]() ,
,
得 ![]() ,
,
解得![]() ,
,
∴二次函数的解析式为![]() ;
;
(2)①∵![]() ,
,
∴顶点M(1,4),
设直线BM的解析式为![]() ,
,
将点B(3,0),M(1,4)代入,
得![]() ,
,
解得 ![]() ,
,
∴直线BM的解析式为![]() ,
,
∵PD⊥x轴且![]() ,
,
∴P(m,﹣2m+6),
∴![]() ,
,
即![]() ,
,
∵点P在线段BM上,且B(3,0),M(1,4),
∴![]() ;
;
②∵![]() ,
,
∵![]() ,
,
∴当![]() 时,S取最大值
时,S取最大值![]() ,
,
∴P(![]() ,3);
,3);
(3)存在,理由如下:
①如图2﹣1,当![]() 时,
时,
∵![]() ,
,
∴四边形CODP为矩形,
∴![]() ,
,
将![]() 代入直线
代入直线![]() ,
,
得![]() ,
,![]()
∴P(![]() ,3);
,3);
②如图2﹣2,当∠PCD=90°时,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴ ,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
解得![]()
![]() (舍去),
(舍去),![]() ,
,
∴P(![]() ,
,![]() ),
),
③当![]() 时,
时,
∵PD⊥x轴,
∴不存在,
综上所述,点P的坐标为(![]() ,3)或(
,3)或(![]() ,
,![]() ).
).





 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案科目:初中数学 来源: 题型:
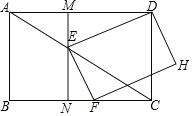
【题目】如图,在矩形ABCD中,AB=3,BC=4,点E是线段AC上的一个动点且![]() =k(0<k<1),点F在线段BC上,且DEFH为矩形;过点E作MN⊥BC,分别交AD,BC于点M,N.
=k(0<k<1),点F在线段BC上,且DEFH为矩形;过点E作MN⊥BC,分别交AD,BC于点M,N.
(1)求证:△MED∽△NFE;
(2)当EF=FC时,求k的值.
(3)当矩形EFHD的面积最小时,求k的值,并求出矩形EFHD面积的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
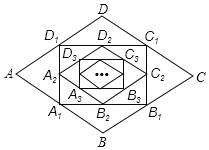
【题目】如图,在菱形ABCD中,边长为1,∠A=60,顺次连接菱形ABCD各边中点,可得四边形A1B1C1D1;顺次连结四边形A1B1C1D1各边中点,可得四边形A2B2C2D2;顺次连结四边形A2B2C2D2各边中点,可得四边形A3B3C3D3;按此规律继续下去,…,则四边形A2019B2019C2019D2019的面积是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
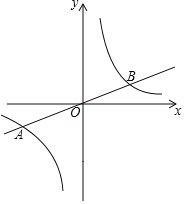
【题目】如图,正比例函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象交于
的图象交于![]() 、
、![]() 两点.
两点.![]() 是第一象限内反比例函数图象上一点,过点
是第一象限内反比例函数图象上一点,过点![]() 作
作![]() 轴的平行线,交直线
轴的平行线,交直线![]() 于点
于点![]() ,连接
,连接![]() ,若
,若![]() 的面积为
的面积为![]() ,则点
,则点![]() 的坐标为_____________.
的坐标为_____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,是二次函数y=ax2+bx+c图象的一部分,其对称轴是x=﹣1,且过点(﹣3,0),下列说法:①abc<0;②2a﹣b=0;③若(﹣5,y1),(3,y2)是抛物线上两点,则y1=y2;④4a+2b+c<0,其中说法正确的( )
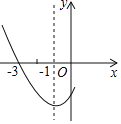
A.①②B.①②③C.①②④D.②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某小型水库栏水坝的横断面是四边形ABCD,DC∥AB,测得迎水坡的坡角α=30°,已知背水坡的坡比为1.2:1,坝顶部DC宽为2m,坝高为6m,则坝底AB的长为_____m.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() 是
是![]() 的反比例函数,下表给出了
的反比例函数,下表给出了![]() 与
与![]() 的一些值.
的一些值.
| … | -4 | -2 | -1 | 1 | 3 | 4 | … | ||
| … | -2 | 6 | 3 | … |
(1)求出这个反比例函数的表达式;
(2)根据函数表达式完成上表;
(3)根据上表,在下图的平面直角坐标系中作出这个反比例函数的图象.
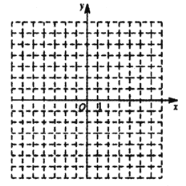
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于
轴交于![]() ,
,![]() 两点(点
两点(点![]() 在
在![]() 轴正半轴上),
轴正半轴上),![]() 为等腰直角三角形,且面积为
为等腰直角三角形,且面积为![]() ,现将抛物线沿
,现将抛物线沿![]() 方向平移,平移后的抛物线过点
方向平移,平移后的抛物线过点![]() 时,与
时,与![]() 轴的另一点为
轴的另一点为![]() ,其顶点为
,其顶点为![]() ,对称轴与
,对称轴与![]() 轴的交点为
轴的交点为![]() .
.
![]() 求
求![]() 、
、![]() 的值.
的值.
![]() 连接
连接![]() ,试判断
,试判断![]() 是否为等腰三角形,并说明理由.
是否为等腰三角形,并说明理由.
![]() 现将一足够大的三角板的直角顶点
现将一足够大的三角板的直角顶点![]() 放在射线
放在射线![]() 或射线
或射线![]() 上,一直角边始终过点
上,一直角边始终过点![]() ,另一直角边与
,另一直角边与![]() 轴相交于点
轴相交于点![]() ,是否存在这样的点
,是否存在这样的点![]() ,使以点
,使以点![]() 、
、![]() 、
、![]() 为顶点的三角形与
为顶点的三角形与![]() 全等?若存在,求出点
全等?若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学课外兴趣小组的同学们要测量被池塘相隔的两棵树A,B的距离,他们设计了如图的测量方案:从树A沿着垂直于AB的方向走到E,再从E沿着垂直于AE的方向走到F,C为AE上一点,其中4位同学分别测得四组数据:①AC,∠ACB;②EF,DE,AD;③CD,∠ACB,∠ADB;④∠F,∠ADB,FB.其中能根据所测数据求得A,B两树距离的有( )
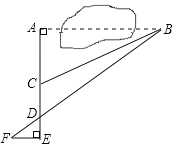
A.1组B.2组C.3组D.4组
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com