
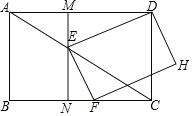
【题目】如图,在矩形ABCD中,AB=3,BC=4,点E是线段AC上的一个动点且![]() =k(0<k<1),点F在线段BC上,且DEFH为矩形;过点E作MN⊥BC,分别交AD,BC于点M,N.
=k(0<k<1),点F在线段BC上,且DEFH为矩形;过点E作MN⊥BC,分别交AD,BC于点M,N.
(1)求证:△MED∽△NFE;
(2)当EF=FC时,求k的值.
(3)当矩形EFHD的面积最小时,求k的值,并求出矩形EFHD面积的最小值.
【答案】(1)见解析;(2)![]() ;(3)矩形EFHD的面积最小值为
;(3)矩形EFHD的面积最小值为![]() ,k=
,k=![]() .
.
【解析】
(1)由矩形的性质得出∠B=90°,AD=BC=4,DC=AB=3,AD∥BC,证出∠EMD=∠FNE=90°,∠NEF=∠MDE,即可得出△MED∽△NFE;
(2)设AM=x,则MD=NC=4﹣x,由三角函数得出ME=![]() x,得出NE=3﹣
x,得出NE=3﹣![]() x,由相似三角形的性质得出
x,由相似三角形的性质得出![]() =
=![]() ,求出NF=
,求出NF=![]() x,得出FC=4﹣x﹣
x,得出FC=4﹣x﹣![]() x=4﹣
x=4﹣![]() x,由勾股定理得出EF=
x,由勾股定理得出EF=![]() =
=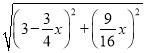 ,当EF=FC时,得出方程4﹣
,当EF=FC时,得出方程4﹣![]() x=
x=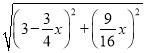 ,解得x=4(舍去),或x=
,解得x=4(舍去),或x=![]() ,进而得出答案;
,进而得出答案;
(3)由相似三角形的性质得出![]() =
=![]() =
=![]() ,得出DE=
,得出DE=![]() EF,求出矩形EFHD的面积=DE×EF=
EF,求出矩形EFHD的面积=DE×EF=![]() EF2=
EF2=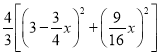 =
= ,由二次函数的性质进而得出答案.
,由二次函数的性质进而得出答案.
(1)证明:∵四边形ABCD是矩形,
∴∠B=90°,AD=BC=4,DC=AB=3,AD∥BC,
∵MN⊥BC,
∴MN⊥AD,
∴∠EMD=∠FNE=90°,
∵四边形DEFH是矩形,
∴∠MED+∠NEF=90°,
∴∠NEF=∠MDE,
∴△MED∽△NFE;
(2)解:设AM=x,则MD=NC=4﹣x,
∵tan∠DAC=tan∠MAE=![]() =
=![]() =
=![]() ,
,
∴ME=![]() x,
x,
∴NE=3﹣![]() x,
x,
∵△MED∽△NFE,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,
,
解得:NF=![]() x,
x,
∴FC=4﹣x﹣![]() x=4﹣
x=4﹣![]() x,EF=
x,EF=![]() =
=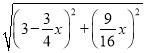 ,
,
当EF=FC时,4﹣![]() x=
x=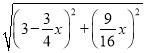 ,
,
解得:x=4或x=![]() ,
,
由题意可知x=4不合题意,
当x=![]() 时,AE=
时,AE=![]() ,
,
∵AC=![]() =
=![]() =5,
=5,
∴k=![]() =
=![]() ;
;
(3)解:由(1)可知:△MED∽△NFE,
∴![]() ,
,
∴DE=![]() EF,
EF,
∴矩形EFHD的面积=DE×EF=![]() EF2=
EF2=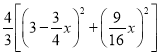 =
=
∴当![]() x﹣
x﹣![]() =0时,即x=
=0时,即x=![]() 时,矩形EFHD的面积最小,最小值为:
时,矩形EFHD的面积最小,最小值为:![]() ,
,
∵cos∠MAE=![]() =
=![]() =
=![]() ,
,
∴AE=![]() AM=
AM=![]() ×
×![]() =
=![]() ,
,
此时k=![]() =
=![]() .
.


 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案科目:初中数学 来源: 题型:
【题目】如图,在由边长为![]() 个单位长度的小正方形组成的
个单位长度的小正方形组成的![]() 网格中,已知点
网格中,已知点![]() ,
,![]() ,
,![]() ,
,![]() 均为网格线的交点.
均为网格线的交点.
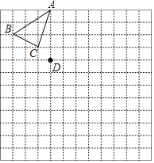
(1)在网格中将![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() ,画出旋转后的图形
,画出旋转后的图形![]() ;
;
(2)在网格中将![]() 放大
放大![]() 倍得到
倍得到![]() ,使
,使![]() 与
与![]() 为对应点.
为对应点.
查看答案和解析>>
科目:初中数学 来源: 题型:
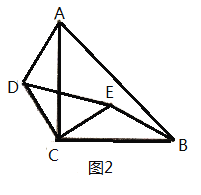
【题目】问题:如图1,等腰直角三角形![]() 中,
中,![]() ,点
,点![]() 、点
、点![]() 分别在
分别在![]() 边上,且
边上,且![]() ,显然
,显然![]() .
.

变式:若将图1中的![]() 绕点
绕点![]() 逆时针旋转,使得点
逆时针旋转,使得点![]() 在
在![]() 的内部,其它条件不变(如图2),请你猜想线段
的内部,其它条件不变(如图2),请你猜想线段![]() 与线段
与线段![]() 的关系,并加以证明.
的关系,并加以证明.
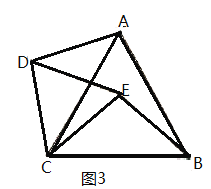
拓展:若图2中的![]() 、
、![]() 都为等边三角形,其它条件不变(如图3),则
都为等边三角形,其它条件不变(如图3),则![]() __________,直线
__________,直线![]() 与
与![]() 相交所夹的锐角为__________°.
相交所夹的锐角为__________°.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从三角形(不是等腰三角形)一个顶点引出一条射线 与对边相交,顶点与交点之间的线段把这个三角形分割成两个小三角形,如果分得的两个小三角形中一个为等腰三角形,另一个与原三角形相似,我们把这条线段叫做这个三角形的完美分割线.
![]() 如图1,在
如图1,在![]() 中,
中,![]() 是
是![]() 的完美分割线,且
的完美分割线,且![]() , 则
, 则![]() 的度数是
的度数是
![]() 如图2,在
如图2,在![]() 中,
中,![]() 为角平分线,
为角平分线,![]() ,求证:
,求证: ![]() 为
为![]() 的完美分割线.
的完美分割线.
![]() 如图2,
如图2,![]() 中,
中,![]() 是
是![]() 的完美分割线,且
的完美分割线,且![]() 是以
是以![]() 为底边的等腰三角形,求完美分割线
为底边的等腰三角形,求完美分割线![]() 的长.
的长.
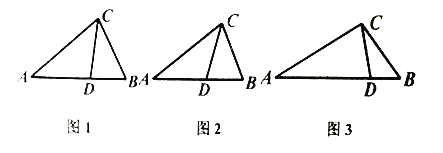
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】只有1和它本身两个因数且大于1的正整数叫做素数.我国数学家陈景润在哥德巴赫猜想的研究中取得了世界领先的成果,哥德巴赫猜想是:每个大于2的偶数都可以表示为两个素数的和,如16=3+ 13.
(1)若从7, 11, 19, 23中随机抽取1个素数,则抽到的素数是7的概率是_______;
(2)若从7, 11, 19, 23中随机抽取1个素数,再从余下的3个数字中随机抽取1个素数,用面树状图或列表的方法求抽到的两个素数之和大于等于30的概率,
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,抛物线y=﹣x2+bx+c经过点A(﹣1,0)和C(0,3).(1)求抛物线的解析式;(2)在抛物线的对称轴上,是否存在点P,使PA+PC的值最小?如果存在,请求出点P的坐标,如果不存在,请说明理由;(3)设点M在抛物线的对称轴上,当△MAC是直角三角形时,求点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
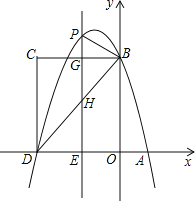
【题目】如图,在平面直角坐标系中,抛物线y=﹣x2+bx+c与x轴交于A、D两点,与y轴交于点B,四边形OBCD是矩形,点A的坐标为(1,0),点B的坐标为(0,4),已知点E(m,0)是线段DO上的动点,过点E作PE⊥x轴交抛物线于点P,交BC于点G,交BD于点H.
(1)求该抛物线的解析式;
(2)当点P在直线BC上方时,请用含m的代数式表示PG的长度;
(3)在(2)的条件下,是否存在这样的点P,使得以P、B、G为顶点的三角形与△DEH相似?若存在,求出此时m的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
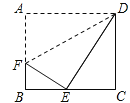
【题目】如图,将矩形纸片ABCD(AD>DC)的一角沿着过点D的直线折叠,使点A与BC边上的点E重合,折痕交AB于点F.若BE:EC=m:n,则AF:FB=
查看答案和解析>>
科目:初中数学 来源: 题型:
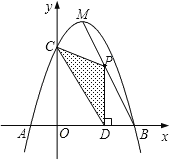
【题目】如图,抛物线y=﹣x2+bx+c与x轴相交于A、B两点,与y轴相交于点C,且点B与点C的坐标分别为B(3,0),C(0,3),点M是抛物线的顶点.
(1)求二次函数的关系式;
(2)点P为线段MB上一个动点,过点P作PD⊥x轴于点D.若OD=m,△PCD的面积为S,
①求S与m的函数关系式,写出自变量m的取值范围.
②当S取得最值时,求点P的坐标;
(3)在MB上是否存在点P,使△PCD为直角三角形?如果存在,请直接写出点P的坐标;如果不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com