
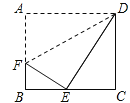
【题目】如图,将矩形纸片ABCD(AD>DC)的一角沿着过点D的直线折叠,使点A与BC边上的点E重合,折痕交AB于点F.若BE:EC=m:n,则AF:FB=
 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案科目:初中数学 来源: 题型:
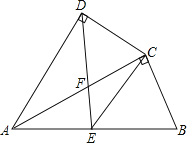
【题目】如图,四边形ABCD中,AC平分∠DAB,∠ADC=∠ACB=90°,E为AB的中点,
(1)求证:AC2=ABAD.
(2)求证:CE∥AD;
(3)若AD=4,AB=6,求AF的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
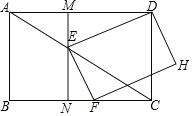
【题目】如图,在矩形ABCD中,AB=3,BC=4,点E是线段AC上的一个动点且![]() =k(0<k<1),点F在线段BC上,且DEFH为矩形;过点E作MN⊥BC,分别交AD,BC于点M,N.
=k(0<k<1),点F在线段BC上,且DEFH为矩形;过点E作MN⊥BC,分别交AD,BC于点M,N.
(1)求证:△MED∽△NFE;
(2)当EF=FC时,求k的值.
(3)当矩形EFHD的面积最小时,求k的值,并求出矩形EFHD面积的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】国庆期间,某风景区推出两种旅游观光活动付费方式:若人数不超过20人,人均缴费500元;若人数超过20人,则每增加一位旅客,人均收费降低10元,但是人均收费不低于350元.现在某单位在国庆期间组织一批贡献突出的职工到该景区旅游观光,支付了12000元观光费,请问:该单位一共组织了多少位职工参加旅游观光活动?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】游泳是一项深受青少年喜爱的体育运动,某中学为了加强学生的游泳安全意识,组织学生观看了纪实片“孩子,请不要私自下水”,并于观看后在本校的![]() 名学生中作了抽样调查.制作了下面两个不完整的统计图.请根据这两个统计图回答以下问题:
名学生中作了抽样调查.制作了下面两个不完整的统计图.请根据这两个统计图回答以下问题:

(I)这次抽样调查中,共调查了 名学生;
(2)补全两个统计图;
(3)根据抽样调查的结果,估算该校![]() 名学生中大约有多少人“结伴时会下河学游泳”?
名学生中大约有多少人“结伴时会下河学游泳”?
查看答案和解析>>
科目:初中数学 来源: 题型:
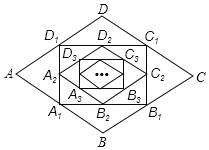
【题目】如图,在菱形ABCD中,边长为1,∠A=60,顺次连接菱形ABCD各边中点,可得四边形A1B1C1D1;顺次连结四边形A1B1C1D1各边中点,可得四边形A2B2C2D2;顺次连结四边形A2B2C2D2各边中点,可得四边形A3B3C3D3;按此规律继续下去,…,则四边形A2019B2019C2019D2019的面积是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
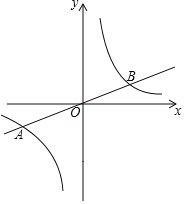
【题目】如图,正比例函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象交于
的图象交于![]() 、
、![]() 两点.
两点.![]() 是第一象限内反比例函数图象上一点,过点
是第一象限内反比例函数图象上一点,过点![]() 作
作![]() 轴的平行线,交直线
轴的平行线,交直线![]() 于点
于点![]() ,连接
,连接![]() ,若
,若![]() 的面积为
的面积为![]() ,则点
,则点![]() 的坐标为_____________.
的坐标为_____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于
轴交于![]() ,
,![]() 两点(点
两点(点![]() 在
在![]() 轴正半轴上),
轴正半轴上),![]() 为等腰直角三角形,且面积为
为等腰直角三角形,且面积为![]() ,现将抛物线沿
,现将抛物线沿![]() 方向平移,平移后的抛物线过点
方向平移,平移后的抛物线过点![]() 时,与
时,与![]() 轴的另一点为
轴的另一点为![]() ,其顶点为
,其顶点为![]() ,对称轴与
,对称轴与![]() 轴的交点为
轴的交点为![]() .
.
![]() 求
求![]() 、
、![]() 的值.
的值.
![]() 连接
连接![]() ,试判断
,试判断![]() 是否为等腰三角形,并说明理由.
是否为等腰三角形,并说明理由.
![]() 现将一足够大的三角板的直角顶点
现将一足够大的三角板的直角顶点![]() 放在射线
放在射线![]() 或射线
或射线![]() 上,一直角边始终过点
上,一直角边始终过点![]() ,另一直角边与
,另一直角边与![]() 轴相交于点
轴相交于点![]() ,是否存在这样的点
,是否存在这样的点![]() ,使以点
,使以点![]() 、
、![]() 、
、![]() 为顶点的三角形与
为顶点的三角形与![]() 全等?若存在,求出点
全等?若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com