
【题目】国庆期间,某风景区推出两种旅游观光活动付费方式:若人数不超过20人,人均缴费500元;若人数超过20人,则每增加一位旅客,人均收费降低10元,但是人均收费不低于350元.现在某单位在国庆期间组织一批贡献突出的职工到该景区旅游观光,支付了12000元观光费,请问:该单位一共组织了多少位职工参加旅游观光活动?
【答案】30
【解析】
设该单位一共组织了x位职工参加旅游观光活动,求出当人数为20时的总费用及人均收费350元时的人数,即可得出20<x<35,再利用总费用=人数×人均收费,即可得出关于x的一元二次方程,解之取其较小值即可得出结论.
解:设该单位一共组织了x位职工参加旅游观光活动,
∵500×20=10000(元),10000<12000,(500﹣350)=15(人),12000÷350=34![]() (人),34
(人),34![]() 不为整数,
不为整数,
∴20<x<20+15,即20<x<35.
依题意,得:x[500﹣10(x﹣20)]=12000,
整理,得:x2﹣70x+1200=0,
解得:x1=30,x2=40(不合题意,舍去).
答:该单位一共组织了30位职工参加旅游观光活动.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,△ABC内接于⊙O,点D在AB边上,CD与OB交于点E,∠ACD=∠OBC;
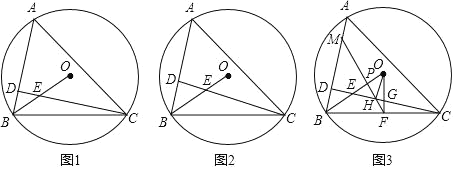
(1)如图1,求证:CD⊥AB;
(2)如图2,当∠BAC=∠OBC+∠BCD时,求证:BO平分∠ABC;
(3)如图3,在(2)的条件下,作OF⊥BC于点F,交CD于点G,作OH⊥CD于点H,连接FH并延长,交OB于点P,交AB边于点M.若OF=3,MH=5,求AC边的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
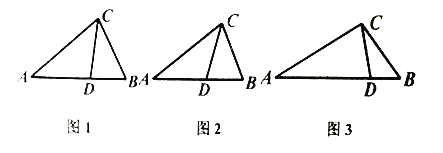
【题目】从三角形(不是等腰三角形)一个顶点引出一条射线 与对边相交,顶点与交点之间的线段把这个三角形分割成两个小三角形,如果分得的两个小三角形中一个为等腰三角形,另一个与原三角形相似,我们把这条线段叫做这个三角形的完美分割线.
![]() 如图1,在
如图1,在![]() 中,
中,![]() 是
是![]() 的完美分割线,且
的完美分割线,且![]() , 则
, 则![]() 的度数是
的度数是
![]() 如图2,在
如图2,在![]() 中,
中,![]() 为角平分线,
为角平分线,![]() ,求证:
,求证: ![]() 为
为![]() 的完美分割线.
的完美分割线.
![]() 如图2,
如图2,![]() 中,
中,![]() 是
是![]() 的完美分割线,且
的完美分割线,且![]() 是以
是以![]() 为底边的等腰三角形,求完美分割线
为底边的等腰三角形,求完美分割线![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
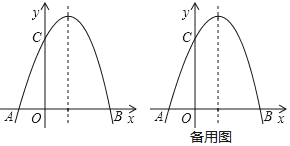
【题目】已知,抛物线y=﹣x2+bx+c经过点A(﹣1,0)和C(0,3).(1)求抛物线的解析式;(2)在抛物线的对称轴上,是否存在点P,使PA+PC的值最小?如果存在,请求出点P的坐标,如果不存在,请说明理由;(3)设点M在抛物线的对称轴上,当△MAC是直角三角形时,求点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
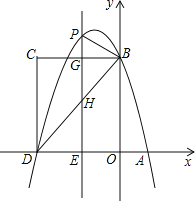
【题目】如图,在平面直角坐标系中,抛物线y=﹣x2+bx+c与x轴交于A、D两点,与y轴交于点B,四边形OBCD是矩形,点A的坐标为(1,0),点B的坐标为(0,4),已知点E(m,0)是线段DO上的动点,过点E作PE⊥x轴交抛物线于点P,交BC于点G,交BD于点H.
(1)求该抛物线的解析式;
(2)当点P在直线BC上方时,请用含m的代数式表示PG的长度;
(3)在(2)的条件下,是否存在这样的点P,使得以P、B、G为顶点的三角形与△DEH相似?若存在,求出此时m的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,分别沿长方形纸片ABCD和正方形纸片EFGH的对角线AC,EG剪开,拼成如图2所示的ALMN,若中间空白部分四边形OPQR恰好是正方形,且ALMN的面积为50,则正方形EFGH的面积为( )
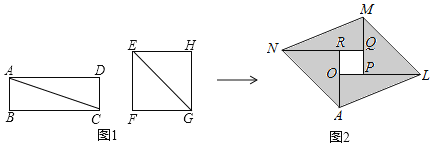
A. 24 B. 25 C. 26 D. 27
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将矩形纸片ABCD(AD>DC)的一角沿着过点D的直线折叠,使点A与BC边上的点E重合,折痕交AB于点F.若BE:EC=m:n,则AF:FB=
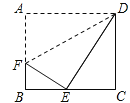
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AB∥DC,BC>AD,∠D=90°,AC⊥BC,AB=10cm,BC=6cm,F点以2cm/秒的速度在线段AB上由A向B匀速运动,E点同时以1cm/秒的速度在线段BC上由B向C匀速运动,设运动时间为t秒(0<t<5).

(1)求证:△ACD∽△BAC;
(2)求DC的长;
(3)试探究:△BEF可以为等腰三角形吗?若能,求t的值;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A.若某种游戏活动的中奖率是![]() ,则参加这种活动10次必有3次中奖
,则参加这种活动10次必有3次中奖
B.可能性很大的事件在一次试验中必然会发生
C.相等的圆心角所对的弧相等是随机事件
D.掷一枚图钉,落地后钉尖“朝上”和“朝下”的可能性相等
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com