
【题目】如图,四边形![]() 内接于圆,
内接于圆,![]() ,
,![]() 的延长线交于点
的延长线交于点![]() ,
,![]() 是
是![]() 延长线上任意一点,
延长线上任意一点,![]() .
.
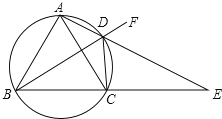
(1)求证:![]() 平分
平分![]() ;
;
(2)求证:![]() .
.
【答案】(1)证明见解析;(2)证明见解析.
【解析】
(1)根据圆内接四边形的性质得到∠CDE=∠ABC,根据圆周角定理和等腰三角形的性质证明即可;
(2)根据三角形外角的性质和图形得到∠CAE+∠E=∠ABD+∠DBC,得到∠E=∠ABD,根据圆周角定理证明即可.
(1)∵四边形ABCD内接于圆,
∴∠CDE=∠ABC.
由圆周角定理得:∠ACB=∠ADB,又∠ADB=∠FDE,
∴∠ACB=∠FDE.
∵AB=AC,
∴∠ACB=∠ABC,
∴∠FDE=∠CDE,即DE平分∠CDF;
(2)∵∠ACB=∠ABC,∠ACB=∠CAE+∠E,∠ABC=∠ABD+∠DBC,
∴∠CAE+∠E=∠ABD+∠DBC.
又∵∠CAE=∠DBC,
∴∠E=∠ABD,
∴∠ACD=∠AEB.


科目:初中数学 来源: 题型:
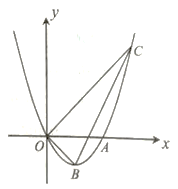
【题目】如图,抛物线![]() 过原点,且与
过原点,且与![]() 轴交于点
轴交于点![]() .
.
(1)求抛物线的解析式及顶点![]() 的坐标;
的坐标;
(2)已知![]() 为抛物线上一点,连接
为抛物线上一点,连接![]() ,
,![]() ,
,![]() ,求
,求![]() 的值;
的值;
(3)在第一象限的抛物线上是否存在一点![]() ,过点
,过点![]() 作
作![]() 轴于点
轴于点![]() ,使以
,使以![]() ,
,![]() ,
,![]() 三点为顶点的三角形与
三点为顶点的三角形与![]() 相似,若存在,求出满足条件的点
相似,若存在,求出满足条件的点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
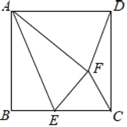
【题目】如图,正方形ABCD的边长为6,点E边BC上,连接AE,将△ABE沿着AE翻折到△AEF,连接CF、DF,若△CDF为等腰三角形,则△CDF的面积为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b与反比例函数y=![]() 的图象相较于A(2,3),B(﹣3,n)两点.
的图象相较于A(2,3),B(﹣3,n)两点.
(1)求一次函数与反比例函数的解析式;
(2)根据所给条件,请直接写出不等式kx+b>![]() 的解集;
的解集;
(3)过点B作BC⊥x轴,垂足为C,求S△ABC.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,是二次函数y=ax2+bx+c图象的一部分,其对称轴是x=﹣1,且过点(﹣3,0),下列说法:①abc<0;②2a﹣b=0;③若(﹣5,y1),(3,y2)是抛物线上两点,则y1=y2;④4a+2b+c<0,其中说法正确的( )
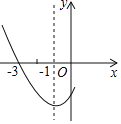
A.①②B.①②③C.①②④D.②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年5月“亚洲文明对话大会”在北京成功举办,引起了世界人民的极大关注,某市一研究机构为了了解10—60岁年龄段市民对本次大会的关注程度,随机选取了100名年龄在该范围内的市民进行了调查,并将收集到的数据制成了如下尚不完整的频数分布表、频数分布走访图和扇形统计图:


(1)请直接写出![]() 、
、![]() 的值及扇形统计图中第3组所对应的圆心角的度数;
的值及扇形统计图中第3组所对应的圆心角的度数;
(2)请补全上面的频数分布直方图;
(3)假设该市现有10—60岁的市民300万人,问第4组年龄段关注本次大会的人数经销商有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,排球运动员站在点O处练习发球,将球从O点正上方2m的A处发出,把球看成点,其运行的高度y(m)与运行的水平距离x(m)满足关系式y=a(x![]() k)2+h.已知球与O点的水平距离为6m时,达到最高2.6m,球网与O点的水平距离为9m.高度为2.43m,球场的边界距O点的水平距离为18m,则下列判断正确的是( )
k)2+h.已知球与O点的水平距离为6m时,达到最高2.6m,球网与O点的水平距离为9m.高度为2.43m,球场的边界距O点的水平距离为18m,则下列判断正确的是( )
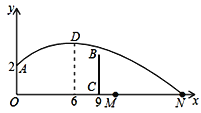
A. 球不会过网 B. 球会过球网但不会出界
C. 球会过球网并会出界 D. 无法确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=k1x+b的图象与反比例函数y=![]() 的图象相交于A,B两点,点A的坐标为(﹣1,3),点B的坐标为(3,n).
的图象相交于A,B两点,点A的坐标为(﹣1,3),点B的坐标为(3,n).
(1)求这两个函数的表达式;
(2)点P在线段AB上,且S△APO:S△BOP=1:3,求点P的坐标.
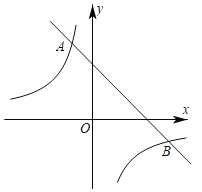
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com