
【题目】如图,在△ABC中,D是BC的中点,DE⊥AB,DF⊥AC,垂足分别是E,F,且BE=CF.求证: 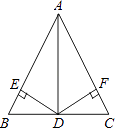
(1)AD是△ABC的角平分线;
(2)AE=AF.
科目:初中数学 来源: 题型:
【题目】某汽车制造厂开发一款新式电动汽车,计划一年生产安装240辆.由于抽调不出足够的熟练工来完成新式电动汽车的安装,工厂决定招聘一些新工人.他们经过培训后上岗,也能独立进行电动汽车的安装.生产开始后,调研部门发现:1名熟练工和2名新工人每月可安装8辆电动汽车;2名熟练工和3名新工人每月可安装14辆电动汽车.
(1)每名熟练工和新工人每月分别可以安装多少辆电动汽车?
(2)如果工厂招聘n(0<n<10)名新工人,使得招聘的新工人和抽调的熟练工刚好能完成一年的安装任务,那么工厂有哪几种新工人的招聘方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax+bx+c(a≠0)的图像如图所示,则下列结论中正确的是( )
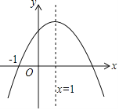
A.a>0 B.3是方程ax+bx+c=0的一个根
C.a+b+c=0 D.当x<1时,y随x的增大而减小
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点D,F在线段AB上,点E,G分别在线段BC和AC上,CD∥EF,∠1=∠2. 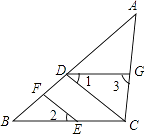
(1)判断DG与BC的位置关系,并说明理由;
(2)若DG是∠ADC的平分线,∠3=85°,且∠DCE:∠DCG=9:10,试说明AB与CD有怎样的位置关系?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在四边形ABCD中,∠DAB被对角线AC平分,且AC2=AB·AD,我们称该四边形为“可分四边形”,∠DAB称为“可分角”.
(1)如图2,四边形ABCD为“可分四边形”,∠DAB为“可分角”,如果∠DCB=∠DAB,则∠DAB=_________.
(2)如图3,在四边形ABCD中,∠DAB=60°,AC平分∠DAB,且∠BCD=150°,求证:四边形ABCD为“可分四边形”;
(3)现有四边形ABCD为“可分四边形”,∠DAB为“可分角”,且AC=4,BC=2,∠D=90°,求AD的长?

图1 图2 图3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com