
【题目】如图,AB是⊙O的切线,B为切点,AC经过点O,与⊙O分别相交于点D,C.若∠ACB=30°,AB= ![]() ,则阴影部分的面积是( )
,则阴影部分的面积是( ) 
A.![]()
B.![]()
C.![]() ﹣
﹣ ![]()
![]()
D.![]() ﹣
﹣ ![]()
![]()
【答案】C
【解析】解:连接OB.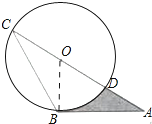
∵AB是⊙O切线,
∴OB⊥AB,
∵OC=OB,∠C=30°,
∴∠C=∠OBC=30°,
∴∠AOB=∠C+∠OBC=60°,
在RT△ABO中,∵∠ABO=90°,AB= ![]() ,∠A=30°,
,∠A=30°,
∴OB=1,
∴S阴=S△ABO﹣S扇形OBD= ![]() ×1×
×1× ![]() ﹣
﹣ ![]() =
= ![]() ﹣
﹣ ![]() .
.
故选C.
【考点精析】本题主要考查了切线的性质定理和扇形面积计算公式的相关知识点,需要掌握切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径;在圆上,由两条半径和一段弧围成的图形叫做扇形;扇形面积S=π(R2-r2)才能正确解答此题.


 孟建平名校考卷系列答案
孟建平名校考卷系列答案科目:初中数学 来源: 题型:
【题目】已知抛物线C:y=x2﹣3x+m,直线l:y=kx(k>0),当k=1时,抛物线C与直线l只有一个公共点.
(1)求m的值;
(2)若直线l与抛物线C交于不同的两点A,B,直线l与直线l1:y=﹣3x+b交于点P,且 ![]() +
+ ![]() =
= ![]() ,求b的值;
,求b的值;
(3)在(2)的条件下,设直线l1与y轴交于点Q,问:是否在实数k使S△APQ=S△BPQ?若存在,求k的值,若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形OABC中,OA=3,OC=2,F是AB上的一个动点(F不与A,B重合),过点F的反比例函数y= ![]() (k>0)的图象与BC边交于点E.
(k>0)的图象与BC边交于点E.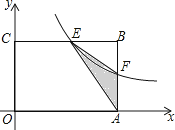
(1)当F为AB的中点时,求该函数的解析式;
(2)当k为何值时,△EFA的面积最大,最大面积是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线y=﹣2x+10与x轴,y轴相交于A,B两点,点C的坐标是(8,4),连接AC,BC.
(1)求过O,A,C三点的抛物线的解析式,并判断△ABC的形状;
(2)动点P从点O出发,沿OB以每秒2个单位长度的速度向点B运动;同时,动点Q从点B出发,沿BC以每秒1个单位长度的速度向点C运动.规定其中一个动点到达端点时,另一个动点也随之停止运动.设运动时间为t秒,当t为何值时,PA=QA?
(3)在抛物线的对称轴上,是否存在点M,使以A,B,M为顶点的三角形是等腰三角形?若存在,求出点M的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解市民对全市创卫工作的满意程度,某中学教学兴趣小组在全市甲、乙两个区内进行了调查统计,将调查结果分为不满意,一般,满意,非常满意四类,回收、整理好全部问卷后,得到下列不完整的统计图.
请结合图中信息,解决下列问题:
(1)求此次调查中接受调查的人数.
(2)求此次调查中结果为非常满意的人数.
(3)兴趣小组准备从调查结果为不满意的4位市民中随机选择2为进行回访,已知4为市民中有2位来自甲区,另2位来自乙区,请用列表或用画树状图的方法求出选择的市民均来自甲区的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com