
 如图,DE是△ABC的中位线,M是DE的中点,CM的延长线交AB于点N,则S△DMN:S△CEM等于
如图,DE是△ABC的中位线,M是DE的中点,CM的延长线交AB于点N,则S△DMN:S△CEM等于 BC,又点M是DE的中点,可以求出DM:BC的值,也就等于MN:NC的值,从而可以得到MN:MC的比值,也就是点N到DE的距离与点C到DE的距离之比,又DM=DE,所以S△DMN:S△CEM=MN:MC.
BC,又点M是DE的中点,可以求出DM:BC的值,也就等于MN:NC的值,从而可以得到MN:MC的比值,也就是点N到DE的距离与点C到DE的距离之比,又DM=DE,所以S△DMN:S△CEM=MN:MC.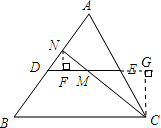 解:∵DE是△ABC的中位线,
解:∵DE是△ABC的中位线, BC,
BC, BC,
BC,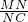 =
= =
= ,
,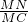 =
=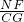 =
= ,
, ,
,

 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com