
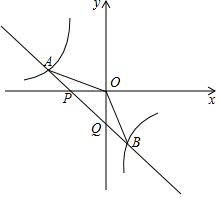
 如图,已知直线y=k1x+b,与x,y轴交于P、Q两点,与y=$\frac{{k}_{2}}{x}$的图象交于A(-2,m),B(1,n)两点,连OA,OB,给出下列结论:
如图,已知直线y=k1x+b,与x,y轴交于P、Q两点,与y=$\frac{{k}_{2}}{x}$的图象交于A(-2,m),B(1,n)两点,连OA,OB,给出下列结论:分析 由一次函数与反比例函数的图象性质即可作出判断.
解答 解:由图象可知:k1<0,k2<0,
∴k1k2>0,故①错误;
∵A(-2,m),B(1,n)两点在反比例函数图象上,
∴k2=-2m=n,
∴-m=$\frac{1}{2}$n,
∴m+$\frac{1}{2}$n=0,故②正确;
令x=0、y=0分别代入y=k1x+b,
∴y=b,x=-$\frac{b}{{k}_{1}}$
∴OQ=-b,OP=$\frac{b}{{k}_{1}}$,
∴S△AOP=$\frac{1}{2}$b×m=$\frac{bm}{2}$
S△BOQ=$\frac{1}{2}$$\frac{b}{{k}_{1}}$×1=$\frac{b}{2{k}_{1}}$
∵k1=$\frac{m-n}{-2-1}$=$\frac{m+2m}{-3}$=-m,
∴S△BOQ=$\frac{1}{2}$$\frac{b}{{k}_{1}}$×1=$\frac{b}{2{k}_{1}}$=$\frac{b}{-2m}$,
∴S△AOP≠S△BOQ,故③错误;
故答案为:②
点评 本题考查反比例函数的图象与性质,解题的关键是根据图象以及解析式求出m、n之间的关系,本题属于中等题型


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com