练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    18．若方程2xm-1+y2n=$\frac{1}{2}$是二元一次方程，则mn=1．

    分析 根据二元一次方程的定义可得m-1=1，2n=1，解方程可得m、n的值，进而代入得到答案．

    解答 解：由题意得：m-1=1，2n=1，
    解得：m=2．n=$\frac{1}{2}$，
    mn=1．
    故答案为：1．

    点评 主要考查二元一次方程的概念，要求熟悉二元一次方程的形式及其特点：含有2个未知数，未知数的项的次数是1的整式方程．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

    8．如图，已知∠1=∠2，要使△ABC≌△ADC，应补充的一个条件是∠BAC=∠DAC（或∠B=∠D或BC=DC）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

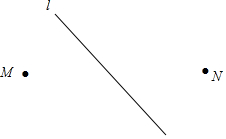    9．2016年7月31日下午，张家口和北京延庆区同时举办“纪念申冬奥成功一周年活动”，并在该活动上表明，张家口要筹划建成一个以崇礼为核心、周边的赤城、张北等为补充的集中连片滑雪大区，形成能让1000万人同时滑雪的区域．如图，规划人员计划在高速公路l旁的大片空地建设M和N两个滑雪场，同时还要建设两条道路使得滑雪场M和N各自到高速公路l的距离都最近，请你帮规划人员设计出这两条道路．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    6．计算（-a2）3的结果是-a6．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    13．如图．抛物线y=-x2+2x+3交x轴于点A（a，0），B（b，0），交y轴于点C，抛物线的顶点为D，点C关于抛物线对称轴的对称点为E，点G、F分别在x轴、y轴上，则四边形EDFG的周长的最小值为（　　）
    A．5+$\sqrt{2}$+$\sqrt{7}$B．5+$\sqrt{2}$+$\sqrt{13}$C．$\sqrt{2}$+$\sqrt{13}$+$\sqrt{17}$D．$\sqrt{2}$+$\sqrt{58}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

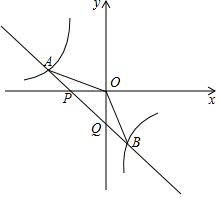    3．如图，已知直线y=k1x+b，与x，y轴交于P、Q两点，与y=$\frac{{k}_{2}}{x}$的图象交于A（-2，m），B（1，n）两点，连OA，OB，给出下列结论：
    ①k1k2＜0     ②m+$\frac{1}{2}$n=0     ③S△AOP=S△BOQ
    其中正确的结论是②．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    10．定义两个实数间的一种运算“*”，这种运算同时满足下列三个条件：①a*b=b*a，②a*0=a，③（a*b）*c=c*a+c*（ab）-2c．有下列结论：
    ①3*1=6；②4*2=12；③（2*3）*0=0；④当x为实数时，有x*$\frac{1}{x}$=x+1．
    其中正确的是①②④．（把所有正确结论的序号都选上）

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    7．已知$\left\{\begin{array}{l}{2x+3y=z}\\{3x+4y=2z+6}\end{array}\right.$且x+y=3，则z的值为（　　）
    A．9B．-3C．12D．不确定

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    8．已知：如图1，菱形ABCD的边长为4cm，P、Q分别是AB、BC两边上的动点，P、Q分别从A、B两点同时出发，均以1cm/s的速度沿AB、BC向点B和点C匀速运动，当点P到达点B时停止运动，点Q也随之停止运动．设运动时间为t（s），点P到AD的距离与点Q到CD的距离差的绝对值为y（cm），且y与t的函数图象如图2所示．

    （1）∠A的度数为60°，M点的坐标所表示的实际意义是点P到AD的距离和点Q到CD的距离相等；
    （2）求证：PD=QD；
    （3）当y=$\frac{\sqrt{3}}{2}$时，求t的值．

    查看答案和解析>>

    同步练习册答案