
 中,
中, ,垂足为
,垂足为 ,
, 是
是 外角
外角 的平分线,
的平分线, ,垂足为
,垂足为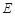 .
.
 为矩形.
为矩形. 满足什么条件时,四边形
满足什么条件时,四边形 是一个正方形?并给出证明.
是一个正方形?并给出证明. 春雨教育同步作文系列答案
春雨教育同步作文系列答案科目:初中数学 来源:不详 题型:解答题
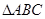 折叠,使点
折叠,使点 与点
与点 重合,这时
重合,这时 为折痕,
为折痕, 为等腰三角形;再继续将纸片沿
为等腰三角形;再继续将纸片沿 的对称轴
的对称轴 折叠,这时得到了两个完全重合的矩形(其中一个是原直角三角形的内接矩形,另一个是拼合成的无缝隙、无重叠的矩形),我们称这样两个矩形为“叠加矩形”.
折叠,这时得到了两个完全重合的矩形(其中一个是原直角三角形的内接矩形,另一个是拼合成的无缝隙、无重叠的矩形),我们称这样两个矩形为“叠加矩形”.
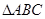 能折叠成“叠加矩形”吗?如果能,请在图②中画出折痕;
能折叠成“叠加矩形”吗?如果能,请在图②中画出折痕; 为一边,画出一个斜三角形
为一边,画出一个斜三角形 ,使其顶点
,使其顶点 在格点上,且
在格点上,且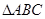 折成的“叠加矩形”为正方形;
折成的“叠加矩形”为正方形;查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 沿
沿 折叠,使
折叠,使 点落在
点落在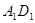 边上的
边上的 点处;再将矩形
点处;再将矩形 沿
沿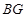 折叠,使
折叠,使 点落在
点落在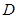 点处且
点处且 过
过 点.
点.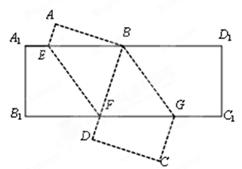
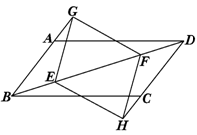
 是平行四边形;
是平行四边形; 是多少度时,四边形
是多少度时,四边形 为菱形?试说明理由.
为菱形?试说明理由.查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
 ,AC = BC,AB = 30,矩形DEFG的一边DE在AB上,顶点G、F分别在AC、BC上,若DG︰GF = 1︰4,则矩形DEFG的面积是 .
,AC = BC,AB = 30,矩形DEFG的一边DE在AB上,顶点G、F分别在AC、BC上,若DG︰GF = 1︰4,则矩形DEFG的面积是 .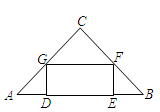
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com