
如图,已知抛物线经过点A(﹣2,0)、B(4,0)、C(0,﹣8).
(1)求抛物线的解析式及其顶点D的坐标;
(2)直线CD交x轴于点E,过抛物线上在对称轴的右边的点P,作y轴的平行线交x轴于点F,交直线CD于M,使PM=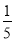 EF,请求出点P的坐标;
EF,请求出点P的坐标;
(3)将抛物线沿对称轴平移,要使抛物线与(2)中的线段EM总有交点,那么抛物线向上最多平移多少个单位长度,向下最多平移多少个单位长度.

(1)抛物线的解析式为y=x2﹣2x﹣8,顶点D的坐标为(1,﹣9);
(2)点P的坐标为(2,﹣8);
(3)要使抛物线与(2)中的线段EM总有交点,抛物线向上最多平移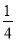 个单位长度,向下最多平移72个单位长度.
个单位长度,向下最多平移72个单位长度.
【解析】
试题分析:(1)由于抛物线与x轴的两个交点已知,抛物线的解析式可设成交点式:y=a(x+2)(x﹣4),然后将点C的坐标代入就可求出抛物线的解析式,再将该解析式配成顶点式,即可得到顶点坐标.
(2)先求出直线CD的解析式,再求出点E的坐标,然后设点P的坐标为(m,n),从而可以用m的代数式表示出PM、EF,然后根据PM=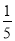 EF建立方程,就可求出m,进而求出点P的坐标.
EF建立方程,就可求出m,进而求出点P的坐标.
(3)先求出点M的坐标,然后设平移后的抛物线的解析式为y=x2﹣2x﹣8+c,然后只需考虑三个临界位置(①向上平移到与直线EM相切的位置,②向下平移到经过点M的位置,③向下平移到经过点E的位置)所对应的c的值,就可以解决问题.
试题解析:(1)根据题意可设抛物线的解析式为y=a(x+2)(x﹣4).
∵点C(0,﹣8)在抛物线y=a(x+2)(x﹣4)上,
∴﹣8a=﹣8.
∴a=1.
∴y=(x+2)(x﹣4)=x2﹣2x﹣8=(x﹣1)2﹣9.
∴抛物线的解析式为y=x2﹣2x﹣8,顶点D的坐标为(1,﹣9);
(2)如图,
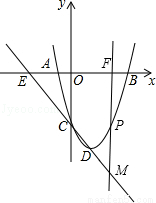
设直线CD的解析式为y=kx+ B.
∴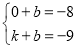
解得: 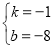 .
.
∴直线CD的解析式为y=﹣x﹣8.
当y=0时,﹣x﹣8=0,
则有x=﹣8.
∴点E的坐标为(﹣8,0).
设点P的坐标为(m,n),
则PM=(m2﹣2m﹣8)﹣(﹣m﹣8)=m2﹣m,EF=m﹣(﹣8)=m+8.
∵PM=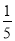 EF,
EF,
∴m2﹣m=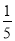 (m+8).
(m+8).
整理得:5m2﹣6m﹣8=0.
∴(5m+4)(m﹣2)=0
解得:m1=﹣ ,m2=2.
,m2=2.
∵点P在对称轴x=1的右边,
∴m=2.
此时,n=22﹣2×2﹣8=﹣8.
∴点P的坐标为(2,﹣8);
(3)当m=2时,y=﹣2﹣8=﹣10.
∴点M的坐标为(2,﹣10).
设平移后的抛物线的解析式为y=x2﹣2x﹣8+c,
①若抛物线y=x2﹣2x﹣8+c与直线y=﹣x﹣8相切,
则方程x2﹣2x﹣8+c=﹣x﹣8即x2﹣x+c=0有两个相等的实数根.
∴(﹣1)2﹣4×1×c=0.
∴c=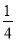 .
.
②若抛物线y=x2﹣2x﹣8+c经过点M,
则有22﹣2×2﹣8+c=﹣10.
∴c=﹣2.
③若抛物线y=x2﹣2x﹣8+c经过点E,
则有(﹣8)2﹣2×(﹣8)﹣8+c=0.
∴c=﹣72.
综上所述:要使抛物线与(2)中的线段EM总有交点,抛物线向上最多平移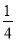 个单位长度,向下最多平移72个单位长度.
个单位长度,向下最多平移72个单位长度.
考点:二次函数综合题.


科目:初中数学 来源:2014年初中毕业升学考试(四川甘孜卷)数学(解析版) 题型:选择题
使代数式 有意义的x的取值范围是( )
有意义的x的取值范围是( )
A.x≥0 B.﹣5≤x<5 C.x≥5 D.x≥﹣5
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(四川成都卷)数学(解析版) 题型:填空题
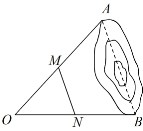
如图,为估计池塘两岸边A,B两点间的距离,在池塘的一侧选取点O,分别去OA、OB的中点M,N,测的MN=32 m,则A,B两点间的距离是 _m.
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(四川德阳卷)数学(解析版) 题型:选择题
已知方程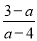 ﹣a=
﹣a=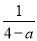 ,且关于x的不等式组
,且关于x的不等式组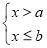 只有4个整数解,那么b的取值范围是( )
只有4个整数解,那么b的取值范围是( )
A.﹣1<b≤3 B.2<b≤3 C.8≤b<9 D.3≤b<4
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(四川宜宾卷)数学(解析版) 题型:解答题
我市中小学全面开展“阳光体育”活动,某校在大课间中开设了A:体操,B:跑操,C:舞蹈,D:健美操四项活动,为了解学生最喜欢哪一项活动,随机抽取了部分学生进行调查,并将调查结果绘制成了如下两幅不完整的统计图,请根据统计图回答下列问题:
(1)这次被调查的学生共有 人.
(2)请将统计图2补充完整.
(3)统计图1中B项目对应的扇形的圆心角是 度.
(4)已知该校共有学生3600人,请根据调查结果估计该校喜欢健美操的学生人数.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com