
【题目】A城有某种农机30台,B城有该农机40台,现要将这些农机全部运往C,D两乡,调运任务承包给某运输公司.已知C乡需要农机34台,D乡需要农机36天,从A城往C,D两乡运送农机的费用分别为250元/台和200元/台,从B城往C,D两乡运送农机的费用分别为150元/台和240元/台.
(1)设A城运往C乡该农机x台,运送全部农机的总费用为W元,求W关于x的函数关系式,并写出自变量x的取值范围;
(2)现该运输公司要求运送全部农机的总费用不低于16460元,则有多少种不同的调运方案?将这些方案设计出来;
(3)现该运输公司决定对A城运往C乡的农机,从运输费中每台减免a元(a≤200)作为优惠,其它费用不变,如何调运,使总费用最少?
【答案】(1)W=140x+12540(0<x≤30);
(2)有3种不同的调运方案,
第一种调运方案:从A城调往C城28台,调往D城2台,从,B城调往C城6台,调往D城34台;
第二种调运方案:从A城调往C城29台,调往D城1台,从,B城调往C城5台,调往D城35台;
第三种调运方案:从A城调往C城30台,调往D城0台,从,B城调往C城4台,调往D城36台,
(3)从A城调往C城30台,调往D城0台,从,B城调往C城4台,调往D城36台.
【解析】分析:(1)A城运往C乡的化肥为x吨,则可得A城运往D乡的化肥为30-x吨,B城运往C乡的化肥为34-x吨,B城运往D乡的化肥为40-(34-x)吨,从而可得出W与x大的函数关系.
(2)根据题意得140x+12540≥16460求得28≤x≤30,于是得到有3种不同的调运方案,写出方案即可;
(3)根据题意得到W=(140-a)x+12540,所以当a=200时,y=-60x+12540,此时x=30时, ![]() =10740元.于是得到结论.
=10740元.于是得到结论.
本题解析:
(1)W=250x+200(30﹣x)+150(34﹣x)+240(6+x)=140x+12540(0<x≤30);
(2)根据题意得140x+12540≥16460,∴x≥28,
∵x≤30,∴28≤x≤30,∴有3种不同的调运方案,
第一种调运方案:从A城调往C城28台,调往D城2台,从,B城调往C城6台,调往D城34台;
第二种调运方案:从A城调往C城29台,调往D城1台,从,B城调往C城5台,调往D城35台;
第三种调运方案:从A城调往C城30台,调往D城0台,从,B城调往C城4台,调往D城36台,
(3)W=x+200(30﹣x)+150(34﹣x)+240(6+x)=x+12540,
所以当a=200时,y最小=﹣60x+12540,此时x=30时y最小=10740元.
此时的方案为:从A城调往C城30台,调往D城0台,从,B城调往C城4台,调往D城36台.


 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案科目:初中数学 来源: 题型:
【题目】实验室里,水平桌面上有甲、乙、丙三个圆柱形容器(容器足够高),底面半径之比为1:2:1,用两个相同的管子在容器的5cm高度处连通(即管子底端离容器底5cm),现三个容器中,只有甲中有水,水位高1cm,如图所示.若每分钟同时向乙和丙注入相同量的水,开始注水1分钟,乙的水位上升![]() cm,则开始注入 分钟的水量后,甲与乙的水位高度之差是0.5cm.
cm,则开始注入 分钟的水量后,甲与乙的水位高度之差是0.5cm.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一块直角三角板DEF放置在△ABC上,三角板DEF的两条直角边DE、DF恰好分别经过点B、C.△ABC中,∠A=50°,求∠DBA+∠DCA的度数. 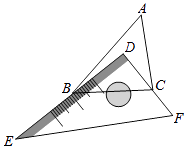
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边CD在正方形ECGF的边CE上,连结BE、DG . 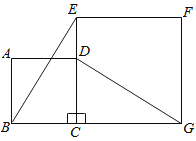
(1)图中是否存在通过旋转能够互相重合的两个三角形?若存在,说出旋转过程;若不存在,请说明理由.
(2)观察猜想BE与DG之间的关系,并证明你的结论.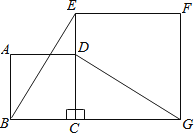
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若∠AOB=45°,P是∠AOB内一点,分别作点P关于直线OA、OB的对称点P1 , P2 , 连接OP1 , OP2 , 则下列结论正确的是( )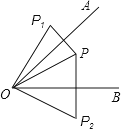
A.OP1⊥OP2
B.OP1=OP2
C.OP1≠OP2
D.OP1⊥OP2且OP1=OP2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com