
某物流公司的甲、乙两辆货车分别从A、B两地同时相向而行,并以各自的速度匀速行驶,途径配货站C,甲车先到达C地,并在C地用1小时配货,然后按原速度开往B地,乙车从B地直达A地,下图是甲、乙两车间的距离 (千米)与乙车出发
(千米)与乙车出发 (时)的函数的部分图像.
(时)的函数的部分图像.
(1)A、B两地的距离是 千米,乙车出发 小时与甲相遇;
(2)求乙车出发1.5小时后直至到达A地的过程中, 与
与 的函数关系式及
的函数关系式及 的取值范围;
的取值范围;
(3)乙车出发多长时间,两车相距100千米?
(1)240;2;(2)分情况讨论见解析;(3)100km.
解析试题分析:(1)根据图象可以知道,在图中A、B两地的距离就是y轴最大值;相遇时间为2小时;(2)根据乙车出发之后的用时进行分类求解:①当 时;②当
时;②当 ;③当
;③当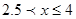 时三个时间段求出函数解析式;(3)根据前面问题的结论可以得到甲、乙的速度分别为80,60;当在1.5小时的时候可知两车的距离为100千米,也可以令两车的距离为100千米即y=100km可以求出x的值,由此可以得到相应的时间段.
时三个时间段求出函数解析式;(3)根据前面问题的结论可以得到甲、乙的速度分别为80,60;当在1.5小时的时候可知两车的距离为100千米,也可以令两车的距离为100千米即y=100km可以求出x的值,由此可以得到相应的时间段.
试题解析:(1)240;2 .
(2)乙车出发1.5小时,y=30,∴过(1.5,30),乙车出发2小时,y="0," ∴过(2,30);乙车出发2.5小时,甲开始运动,此时y=30,∴过(2.5,30),乙车出发4小时,甲乙分别到达目的地,此时y="240," ∴过(4,240)
①当 时,
时, ,解之得
,解之得 ,∴y=-60x+120,
,∴y=-60x+120,
②当 时,
时, ,解之得
,解之得 ,∴y=60x-120,
,∴y=60x-120,
③当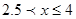 时,
时, ,解之得
,解之得 ,∴y=140x-320,
,∴y=140x-320,
(3)甲、乙的速度分别为80,60,∴在1.5小时前,当 时,相距100km,
时,相距100km,
当x>2.5时,把y=100代入y=140x-320解得x=3,即3小时的时候,相距100km.
考点:一次函数的应用


科目:初中数学 来源: 题型:解答题
周末,小明骑自行车从家里出发到野外郊游.从家出发0.5小时后到达甲地,游玩一段时间后按原速前往乙地,小明离家1小时20分钟后,妈妈驾车沿相同路线前往乙地,如图是他们离家的路程y(km)与小明离家时间x(h)的函数图象,已知妈妈驾车的速度是小明骑车速度的3倍.
(1)求小明骑车的速度和在甲地游玩的时间;
(2)小明从家出发多少小时后被妈妈追上?此时离家多远?
(3)若妈妈比小明早10分钟到达乙地,求从家到乙地的路程.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
某文具店准备购进甲,乙两种钢笔,若购进甲种钢笔100支,乙种钢笔50支,需要1000元,若购进甲种钢笔50支,乙种钢笔30支,需要550元.
(1)求购进甲,乙两种钢笔每支各需多少元?
(2)若该文具店准备拿出1000元全部用来购进这两种钢笔,考虑顾客需求,要求购进甲中钢笔的数量不少于乙种钢笔数量的6倍,且不超过乙种钢笔数量的8倍,那么该文具店共有几种进货方案?
(3)若该文具店销售每支甲种钢笔可获利润2元,销售每支乙种钢笔可获利润3元,在第(2)问的各种进货方案中,哪一种方案获利最大?最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
已知一次函数y=kx+b的图象经过点(-2,-4),且与正比例函数y= x的图象相交于点(4,a),求:
x的图象相交于点(4,a),求:
(1)a的值;
(2)k、b的值;
(3)这两个函数的图象与y轴相交得到的三角形的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,四边形OABC是矩形,点A、C的坐标分别为(3,0)、(0,1),点D是线段BC上的动点(与端点B、C不重合),过点D作直线 交折线OAB于点E.
交折线OAB于点E.
(1)记 的面积为S,求S与b的函数关系式;
的面积为S,求S与b的函数关系式;
(2)当点E在线段OA上时,若矩形OABC关于直线DE的对称图形为四边形 ,DE=
,DE= ,试探究四边形
,试探究四边形 与矩形OABC的重叠部分的面积是否发生变化,若不变,求出该重叠部分的面积;若改变,请说明理由。
与矩形OABC的重叠部分的面积是否发生变化,若不变,求出该重叠部分的面积;若改变,请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
在一次蜡烛燃烧试验中,甲、乙两根蜡烛燃烧时剩余部分的高度y(厘米)与燃烧时间x(小时)之间的关系如图所示,请根据图象所提供的信息解答下列问题:
(1)甲、乙两根蜡烛燃烧前的高度分别是 , 从点燃到燃尽所用的时间分别 。
(2)分别求甲、乙两根蜡烛燃烧时y与x之间的函数关系式;
(3)燃烧多长时间时,甲、乙两根蜡烛的高度相等(不考虑都燃尽时的情况)?在什么事件段内,甲蜡烛比乙蜡烛高?在什么时间段内,甲蜡烛比乙蜡烛低?
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
某工厂现有甲种原料360kg,乙种原料290kg,计划用它们生产A、B两种产品共50件,已知每生产一件A种产品,需要甲种原料9kg、乙种原料3kg,获利700元,生产一件B种产品,需要甲种原料4kg、乙种原料10kg,可获利1200元.
(1)利用这些原料,生产A、B两种产品,有哪几种不同的方案?
(2)设生产两种产品总利润为y(元),其中生产A中产品x(件),试写出y与x之间的函数解析式.
(3)利用函数性质说明,采用(1)中哪种生产方案所获总利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,一次函数 与反比例函数
与反比例函数 的图象相交于点A,且点A的纵坐标为1.
的图象相交于点A,且点A的纵坐标为1.
(1)求反比例函数的解析式;
(2)根据图象写出当x>0时,一次函数的值大于反比例函数的值的x的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com