
某文具店准备购进甲,乙两种钢笔,若购进甲种钢笔100支,乙种钢笔50支,需要1000元,若购进甲种钢笔50支,乙种钢笔30支,需要550元.
(1)求购进甲,乙两种钢笔每支各需多少元?
(2)若该文具店准备拿出1000元全部用来购进这两种钢笔,考虑顾客需求,要求购进甲中钢笔的数量不少于乙种钢笔数量的6倍,且不超过乙种钢笔数量的8倍,那么该文具店共有几种进货方案?
(3)若该文具店销售每支甲种钢笔可获利润2元,销售每支乙种钢笔可获利润3元,在第(2)问的各种进货方案中,哪一种方案获利最大?最大利润是多少元?
(1)5,10;(2)6;(3)当y=20时,W有最大值,最大值为380.
解析试题分析:(1)先设购进甲,乙两种钢笔每支各需a元和b元,根据购进甲种钢笔100支,乙种钢笔50支,需要1000元,若购进甲种钢笔50支,乙种钢笔30支,需要550元列出方程组,求出a,b的值即可;
(2)先设购进甲钢笔x支,乙钢笔y支,根据题意列出5x+10y=1000和不等式组6y≤x≤8y,把方程代入不等式组即可得出20≤y≤25,求出y的值即可;
(3)先设利润为W元,得出W=2x+3y=400-y,根据一次函数的性质求出最大值.
试题解析:(1)设购进甲,乙两种钢笔每支各需a元和b元,根据题意得: ,
,
解得: ,
,
答:购进甲,乙两种钢笔每支各需5元和10元;
(2)设购进甲钢笔x支,乙钢笔y支,根据题意可得: ,
,
解得:20≤y≤25,
∵x,y为整数,
∴y=20,21,22,23,24,25共六种方案,
∵5x=1000-10y>0,
∴0<y<100,
∴该文具店共有6种进货方案;
(3)设利润为W元,则W=2x+3y,
∵5x+10y=1000,
∴x=200-2y,
∴代入上式得:W=400-y,
∵W随着y的增大而减小,
∴当y=20时,W有最大值,最大值为W=400-20=380(元).
考点: 1.一元一次不等式组的应用;2.二元一次方程组的应用.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
在平面直角坐标系xOy中,对于任意两点P1(x1,y1)与P2(x2,y2)的“非常距离”,给出如下定义:
若|x1﹣x2|≥|y1﹣y2|,则点P1与点P2的“非常距离”为|x1﹣x2|;
若|x1﹣x2|<|y1﹣y2|,则点P1与点P2的“非常距离”为|y1﹣y2|.
例如:点P1(1,2),点P2(3,5),因为|1﹣3|<|2﹣5|,所以点P1与点P2的“非常距离”为|2﹣5|=3,也就是图1中线段P1Q与线段P2Q长度的较大值(点Q为垂直于y轴的直线P1Q与垂直于x轴的直线P2Q交点).
(1)已知点A(﹣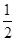 ,0),B为y轴上的一个动点,
,0),B为y轴上的一个动点,
①若点A与点B的“非常距离”为2,写出一个满足条件的点B的坐标;
②直接写出点A与点B的“非常距离”的最小值;
(2)已知C是直线y= x+3上的一个动点,
x+3上的一个动点,
①如图2,点D的坐标是(0,1),求点C与点D的“非常距离”的最小值及相应的点C的坐标;
②如图3,E是以原点O为圆心,1为半径的圆上的一个动点,求点C与点E的“非常距离”的最小值及相应的点E与点C的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
为保护学生视力,课桌椅的高度都是按一定的关系配套设计的,研究表明:假设课桌的高度为 cm,椅子的高度为
cm,椅子的高度为 cm,则
cm,则 应是
应是 的一次函数,下表列出两套符合条件的课桌椅的高度:
的一次函数,下表列出两套符合条件的课桌椅的高度:
| | 第一套 | 第二套 |
椅子高度 (cm) (cm) | 40 | 37 |
课桌高度 (cm) (cm) | 75 | 70 |
 与
与 的函数关系式.
的函数关系式.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,已知反比例函数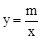 (m是常数,m≠0),一次函数y=ax+b(a、b为常数,a≠0),其中一次函数与x轴,y轴的交点分别是A(-4,0),B(0,2).
(m是常数,m≠0),一次函数y=ax+b(a、b为常数,a≠0),其中一次函数与x轴,y轴的交点分别是A(-4,0),B(0,2).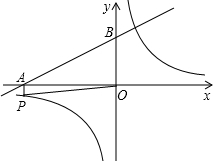
(1)求一次函数的关系式;
(2)反比例函数图象上有一点P满足:①PA⊥x轴;②PO= (O为坐标原点),求反比例函数的关系式;
(O为坐标原点),求反比例函数的关系式;
(3)求点P关于原点的对称点Q的坐标,判断点Q是否在该反比例函数的图象上.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,直线AB与坐标轴分别交于点A、点B,且OA、OB的长分别为方程x2-6x+8=0的两个根(OA<OB),点C在y轴上,且OA︰AC=2︰5,直线CD垂直于直线AB于点P,交x轴于点D.
(1)求出点A、点B的坐标.
(2)请求出直线CD的解析式.
(3)若点M为坐标平面内任意一点,在坐标平面内是否存在这样的点M,使以点B、P、D、M为顶点的四边形是平行四边形?若存在,请直接写出点M的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
某物流公司的甲、乙两辆货车分别从A、B两地同时相向而行,并以各自的速度匀速行驶,途径配货站C,甲车先到达C地,并在C地用1小时配货,然后按原速度开往B地,乙车从B地直达A地,下图是甲、乙两车间的距离 (千米)与乙车出发
(千米)与乙车出发 (时)的函数的部分图像.
(时)的函数的部分图像.
(1)A、B两地的距离是 千米,乙车出发 小时与甲相遇;
(2)求乙车出发1.5小时后直至到达A地的过程中, 与
与 的函数关系式及
的函数关系式及 的取值范围;
的取值范围;
(3)乙车出发多长时间,两车相距100千米?
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
(1)观察与发现:将矩形纸片AOCB折叠,使点C与点A重合,点B落在点B′处(如图),折痕为EF.小明发现△AEF为等腰三角形,你同意吗?请说明理由.
(2)实践与应用:以点O为坐标原点,分别以矩形的边OC、OA为x轴、y轴建立如图所示的直角坐标系,若顶点B的坐标为(9,3),请求出折痕EF的长及EF所在直线的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图表示一个正比例函数与一个一次函数的图象,它们交于点A(4,3),一次函数的图象与 轴交于点B,且OA=OB,求这两个函数的关系式及两直线与
轴交于点B,且OA=OB,求这两个函数的关系式及两直线与 轴围成的三角形的面积.
轴围成的三角形的面积. 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com