
分析 (1)由△ABC是正三角形,得出a=b=c,得出a2+b2=2c2,b2+c2=2a2,a2+c2=2b2,即可得出结论;
(2)由勾股定理得出a2+b2=c2,再由已知条件得出c2+a2=2b2,证出2a2+b2=2b2,得出b=$\sqrt{2}$a,c=$\sqrt{3}$a,即可得出结论;
(3)根据题意得出F(k,1),E(2,$\frac{k}{2}$),由矩形的性质和勾股定理得出OF2=1+k2,OE2=4+$\frac{{k}^{2}}{4}$,EF2=BF2+BE2=$\frac{5}{4}{k}^{2}$-5k+5;分三种情况:①当OF2+OE2=4EF2时;②当OF2+EF2=4OE2时;③当OE2+EF2=4OF2时;分别得出关于k的方程,解方程即可.
解答 解:(1)正三角形是2阶三角形;理由如下:
∵△ABC是正三角形,
∴a=b=c,
∴a2+b2=2c2,b2+c2=2a2,a2+c2=2b2,
∴正三角形是2阶三角形;
(2)∵△ABC为2阶直角三角形,
∴a2+b2=c2,且c2+a2=2b2,
∴2a2+b2=2b2,
∴b=$\sqrt{2}$a,
∴c=$\sqrt{3}$a,
∴a:b:c=1:$\sqrt{2}$:$\sqrt{3}$;
(3)如图所示: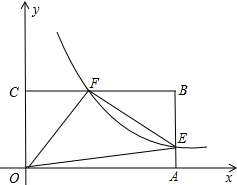 根据题意得:F(k,1),E(2,$\frac{k}{2}$),
根据题意得:F(k,1),E(2,$\frac{k}{2}$),
∵四边形ABCO是矩形,
∴∠OCF=∠B=∠OAB=90°,
∴OF2=1+k2,OE2=4+$\frac{{k}^{2}}{4}$,EF2=BF2+BE2=(2-k)2+(1-$\frac{k}{2}$)2=$\frac{5}{4}{k}^{2}$-5k+5;
分三种情况:①当OF2+OE2=4EF2时,1+k2+4+$\frac{{k}^{2}}{4}$=4($\frac{5}{4}{k}^{2}$-5k+5),
解得:k=$\frac{8±2\sqrt{7}}{3}$;
②当OF2+EF2=4OE2时,1+k2+$\frac{5}{4}{k}^{2}$-5k+5=4(4+$\frac{{k}^{2}}{4}$),
解得:k=2±2$\sqrt{3}$(负值舍去),
∴k=2+2$\sqrt{3}$;
③当OE2+EF2=4OF2时,4+$\frac{{k}^{2}}{4}$+$\frac{5}{4}{k}^{2}$-5k+5=4(1+k2),
解得:k=-1±$\sqrt{3}$(负值舍去),
∴k=-1+$\sqrt{3}$;
综上所述:k的值为$\frac{8±2\sqrt{7}}{3}$,或2+2$\sqrt{3}$,或-1+$\sqrt{3}$.
点评 本题是反比例函数综合题目,考查了正三角形的性质、坐标与图形性质、勾股定理、矩形的性质、一元二次方程的解法以及n阶三角形的定义等知识;本题难度较大,综合性强,特别是(3)中,需要进行分类讨论,根据勾股定理列出方程,解方程才能得出结果.


科目:初中数学 来源: 题型:解答题
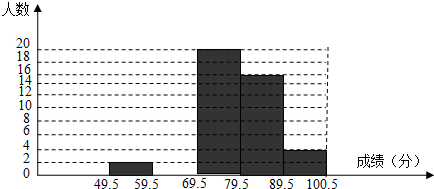
| 分组 | 49.5~59.5 | 59.5~69.5 | 69.5~79.5 | 79.5~89.5 | 89.5~100.5 | 合计 |
| 频数 | 2 | A | 20 | 16 | 4 | 50 |
| 频率 | 0.04 | 0.16 | 0.40 | 0.32 | B | 1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com