

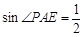 ③HP//AE ④HF=1 ⑤
③HP//AE ④HF=1 ⑤
| A.2个 | B.3个 | C.4个 | D.5个 |
 则可证明M为AB中等,故Rt△AEM≌Rt△BEM,则AE=BE。
则可证明M为AB中等,故Rt△AEM≌Rt△BEM,则AE=BE。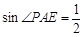 正确:因为正方形ABCD中,E为CD中点,所以Rt△ADE中,AD=2DE,所以
正确:因为正方形ABCD中,E为CD中点,所以Rt△ADE中,AD=2DE,所以 ,所以
,所以
 ,但∠EPA并不等于90°,所以②不正确;
,但∠EPA并不等于90°,所以②不正确;

 NE=2,
NE=2, PM,故可得HF=
PM,故可得HF=




 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源:不详 题型:单选题

查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题

查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
 ,∠B=45°.直角三角板含45°角的顶点E在边BC上移动,一直角边始终经过点A,斜边与CD交于点F,若△ABE是以AB为腰的等腰三角形,则CF= .
,∠B=45°.直角三角板含45°角的顶点E在边BC上移动,一直角边始终经过点A,斜边与CD交于点F,若△ABE是以AB为腰的等腰三角形,则CF= .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com