Question

【题目】A校和B校分别库存有电脑12台和6台，现决定支援给C校10台和D校8台．已知从A校调运一台电脑到C校和D校的运费分别为40元和10元；从B校调运一台电脑到C校和D校的运费分别为30元和20元．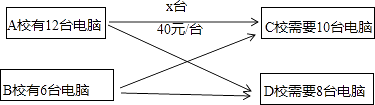
（1）设A校运往C校的电脑为x台，请仿照下图，求总运费W（元）关于x的函数关系式；
（2）求出总运费最低的调运方案，最低运费是多少？

Answer 1

【答案】
（1）解：∵从A校调往C校x台，

∴从A校调往D校（12﹣x）台，从B校调往C校（10﹣x）台，调往D校[6﹣（10﹣x）]=（x﹣4）台，

∴W=40x+10（12﹣x）+30（10﹣x）+20（x﹣4）=20x+340，

∵机器的台数只能是正整数，

∴12﹣x≥0且 10﹣x≥0 且 x﹣4≥0

解得：4≤x≤10，且x为正整数，

∴运费W关于x的函数关系式为：W=20x+340 （4≤x≤10）

（2）解：∵W=20x+340（4≤x≤10）是一次函数，

∴当x=4时，运费W最低，此时W=420，

即总运费最低的调运方案是：从A校调运4台电脑到C校，调运8台电脑到D校，从B校调运6台电脑到C校，最低费用是420元

【解析】（1）根据题意可以求得总运费W（元）关于x的函数关系式，注意x必须是非负整数；（2）根据（1）中的函数关系和一次函数的性质可以解答本题．