
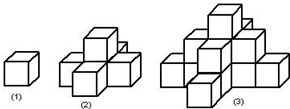
分析 由图形可知:第1个叠放的图形中,小正方体木块个数有1个;第2个叠放的图形中,小正方体木块个数有1+1+4=6个;第3个叠放的图形中,小正方体木块个数应有1+1+4+1+2×4=15个…由此规律得出第n个叠放的图形中,小正方体木块个数应有1+1+1×4+1+2×4+1+3×4+…+1+4(n-1)=n+4×$\frac{1}{2}$n(n-1)=2n2-n个,进一步代入求得答案即可.
解答 解:∵第1叠放的图形中,小正方体木块个数有1个;
第2个叠放的图形中,小正方体木块个数有1+1+4=6个;
第3个叠放的图形中,小正方体木块个数应有1+1+4+1+2×4=15个;
…
∴第n个叠放的图形中,小正方体木块个数应有1+1+1×4+1+2×4+1+3×4+…+1+4(n-1)=n+4×$\frac{1}{2}$n(n-1)=2n2-n个,
∴第4个叠放的图形中,小正方体木块个数应是2×42-4=28个.
故答案为:28,2n2-n.
点评 此题考查图形的变化规律,找出图形之间的联系,得出数字之间的运算规律,利用规律解决问题.


 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案科目:初中数学 来源: 题型:填空题
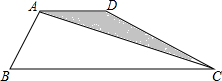 如图,四边形ABCD中,AB=AD,AD∥BC,∠ABC=60°,∠BCD=30°,BC=6,那么△ACD的面积是$\sqrt{3}$.
如图,四边形ABCD中,AB=AD,AD∥BC,∠ABC=60°,∠BCD=30°,BC=6,那么△ACD的面积是$\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
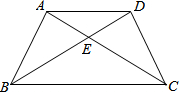 如图,在四边形ABCD中,AB=AD,AC与BD交于点E,∠ADB=∠ACB.
如图,在四边形ABCD中,AB=AD,AC与BD交于点E,∠ADB=∠ACB.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1cm | B. | 5cm | C. | 1cm或5cm | D. | 无法确定 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com