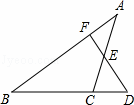
如图，已知D为△ABC边BC延长线上一点，DF⊥AB于F交AC于E，∠A=35°，∠D=50°，求∠ACD的度数．
科目：初中数学 来源： 题型：
阅读下面材料：小强遇到这样一个问题：
试作一个直角△ABC，使∠C=90°，AB=7，AC+BC=9.
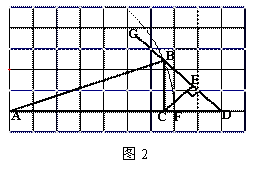
小强是这样思考的：如图1，假定直角△ABC已作出，延长AC到点D，使CD=CB，则AD=9，∠D=45°，因此可先作出一个辅助△ABD，再作BD的垂直平分线分别交AD于点C，BD于点E，连接BC,所得的△ABC即为所作三角形.具体做法小强是利用图2中1
1正方形网格，通过尺规作图完成
的.
（1）请回答：图2中线段AB等于线段 .
（2）
参考小强的方法，解决问题：请在图
3的菱形网格中（菱形最小内角为
，
边长为a），画出一个△ABC，使∠C=，AB=6b，AC+BC=8b.（在图中标明字母，不写作法，保留作图痕迹）.
 | |||
 | |||
‘
查看答案和解析>>
科目：初中数学 来源： 题型：
某班一次数学竞赛考试成绩如下表所示，已知全班共有38人，且众数为60分，中位数为70分，则x2－2y= _．
| 成绩（分） | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 |
| 人数 | 2 | 3 | 5 | x | 6 | y | 3 | 4 |
查看答案和解析>>
科目：初中数学 来源： 题型：
已知，如图，△ABC中，AB=AC，
AD是角平分线，BE=CF，则下列说法正确的有几个
（1）DA平分∠EDF；（2）△EBD≌△FCD；（3）△AED≌△AFD；（4）AD垂直BC．（）
A． 1个 B． 2个 C． 3个 D． 4个
查看答案和解析>>
科目：初中数学 来源： 题型：
已知，矩形ABCD中，AB=4cm，BC=8cm，AC的垂直平分线EF分别交AD、BC于点E、F，垂足为O．
（1）如图1，连接AF、CE．求证四边形AFCE为菱形，并求AF的长；
（2）如图2，动点P、Q分别从A、C两点同时出发，沿△AFB和△CDE各边匀速运动一周．即点P自A→F→B→A停止，点Q自C→D→E→C停止．在运动过程中，
①已知点P的速度为每秒5cm，点Q的速度为每秒4cm，运动
时间为t秒，当A、C、P、Q四点为顶点的四边形是平行四边形时，求t的值．
②若点P、Q的运动路程分别为a、b（单位：cm，ab≠0），已知A、C、P、Q四点为顶点的四边形是平行四边形，求a与b满足的数量关系式．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
