已知抛物线y=-x2-(2m+2)x-(m2+4m-3)与y轴交于点C,与x轴的两个交点A(x1,0),B(1,0)在原点的两旁.
(1)求m的值及抛物线的顶点P的坐标;
(2)设过A、B、C三点的圆O′与直线y=-x-3交于点E.
①试判断△BCE的形状,并证明你的结论;
②求△ACE的面积.
解:(1)∵B(1,0)在抛物线y=-x
2-(2m+2)x-(m
2+4m-3)上,
∴0=-1-2m-2-m
2-4m+3,
解得m=0或-6,
当m=-6时,抛物线y=-x
2+10x-9,此时A、B两点在原点一侧,
∴m=0,
∴抛物线y=-x
2-2x+3=-(x+1)
2+4,
∴抛物线的顶点坐标P(-1,4);
(2)①由题意可知圆心O′在线段AB的垂直平分线上,
又知AB的垂直平分线是抛物线的对称轴,
故可设O′坐标为(-1,y),C点坐标为(0,3),B点坐标为(1,0),
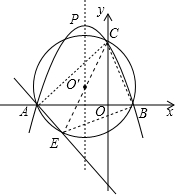
∵O′A=O′B,
∴1+(y-3)
2=4+y
2,
解得y=1,
∴圆心O′坐标为(-1,1),
∴圆的方程为(x+1)
2+(y-1)
2=5,
又∵圆O′与直线y=-x-3交于点E,
∴
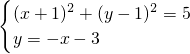
,
解得x
1=-3,x
2=-2,
∴E点坐标为(-2,-1),
∴设直线CE的方程为y=kx+b,
∴
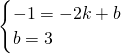
,
解得k=2,
∴直线CE方程为y=2x-3,
∵点O′坐标为(-1,1),
∴该点在直线CE上,
∴C、O′E三点共线,
∴CE为⊙O′的直径,
∴∠CBE=90°,
∴△BCE为直角三角形;
②∵CE是⊙O′直径,
∴∠CAE是直角,
AE=
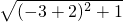
=

,AC=
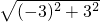
=3

,
∴S△ACE=

AE•AC=

×

×3

=3.
分析:(1)把B点(1,0)代入抛物线y=-x
2-(2m+2)x-(m
2+4m-3)解出m的值,然后根据A、B两点在原点两旁判断出m的值.
(2)①由题意可知圆心O′在线段AB的垂直平分线上,又知AB的垂直平分线是抛物线的对称轴,故可设O′坐标为(-1,y),C点坐标为(0,3),B点坐标为(1,0),求出O′的坐标,进而求出圆的半径,联立直线y=-x-3与圆方程求出E点的坐标,再证明CE是圆的直径,进而判断出△BCE的形状;
②由CE是直径,可知∠CAE是直角,然后根据两点间距离公式求出AC和AE的长,再根据直角三角形面积公式求出△ACE的面积.
点评:本题主要考查二次函数的知识点,涉及了圆方程的求法,三角形形状的判断,三角形面积的求解,此题综合性较大,此题难度也较大,特别是(2)问需要熟练掌握直线与圆的相关知识.


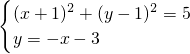 ,
,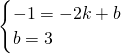 ,
,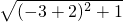 =
= ,AC=
,AC=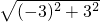 =3
=3 ,
, AE•AC=
AE•AC= ×
× ×3
×3 =3.
=3.

 (1)求b+c的值;
(1)求b+c的值; (2012•虹口区一模)如图,在平面直角坐标系xOy中,已知抛物线y=x2+bx+c经过A(0,3),B(1,0)两点,顶点为M.
(2012•虹口区一模)如图,在平面直角坐标系xOy中,已知抛物线y=x2+bx+c经过A(0,3),B(1,0)两点,顶点为M.