
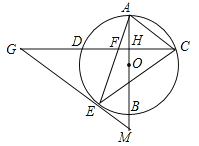
【题目】如图,AB是⊙O的直径,弦CD⊥AB,垂足为H,连结AC,过![]() 上一点E作EG∥AC交CD的延长线于点G,连结AE交CD于点F,且EG=FG,连结CE.
上一点E作EG∥AC交CD的延长线于点G,连结AE交CD于点F,且EG=FG,连结CE.
(1)求证:△ECF∽△GCE;
(2)求证:EG是⊙O的切线;
(3)延长AB交GE的延长线于点M,若tanG=![]() ,AH=
,AH=![]() ,求EM的值.
,求EM的值.
【答案】(1)证明见解析;(2)证明见解析;(3)![]() .
.
【解析】
试题分析:(1)由AC∥EG,推出∠G=∠ACG,由AB⊥CD推出![]() ,推出∠CEF=∠ACD,推出∠G=∠CEF,由此即可证明;
,推出∠CEF=∠ACD,推出∠G=∠CEF,由此即可证明;
(2)欲证明EG是⊙O的切线只要证明EG⊥OE即可;
(3)连接OC.设⊙O的半径为r.在Rt△OCH中,利用勾股定理求出r,证明△AHC∽△MEO,可得![]() ,由此即可解决问题;
,由此即可解决问题;
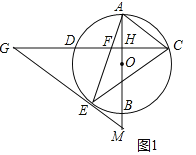
试题解析:(1)证明:如图1.∵AC∥EG,∴∠G=∠ACG,∵AB⊥CD,∴![]() ,∴∠CEF=∠ACD,∴∠G=∠CEF,∵∠ECF=∠ECG,∴△ECF∽△GCE.
,∴∠CEF=∠ACD,∴∠G=∠CEF,∵∠ECF=∠ECG,∴△ECF∽△GCE.
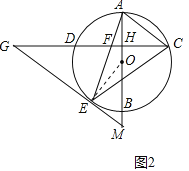
(2)证明:如图2中,连接OE.∵GF=GE,∴∠GFE=∠GEF=∠AFH,∵OA=OE,∴∠OAE=∠OEA,∵∠AFH+∠FAH=90°,∴∠GEF+∠AEO=90°,∴∠GEO=90°,∴GE⊥OE,∴EG是⊙O的切线.
(3)解:如图3中,连接OC.设⊙O的半径为r.
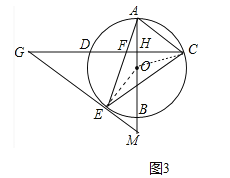
在Rt△AHC中,tan∠ACH=tan∠G=![]() =
=![]() ,∵AH=
,∵AH=![]() ,∴HC=
,∴HC=![]() ,在Rt△HOC中,∵OC=r,OH=r﹣
,在Rt△HOC中,∵OC=r,OH=r﹣![]() ,HC=
,HC=![]() ,∴
,∴![]() ,∴r=
,∴r=![]() ,∵GM∥AC,∴∠CAH=∠M,∵∠OEM=∠AHC,∴△AHC∽△MEO,∴
,∵GM∥AC,∴∠CAH=∠M,∵∠OEM=∠AHC,∴△AHC∽△MEO,∴![]() ,∴
,∴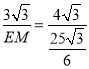 ,∴EM=
,∴EM=![]() .
.


 小学教材完全解读系列答案
小学教材完全解读系列答案科目:初中数学 来源: 题型:
【题目】在开展“经典阅读”活动中,某学校为了解全校学生利用课外时间阅读的情况,学校团委随机抽取若干名学生,调查他们一周的课外阅读时间,并根据调查结果绘制了如下尚不完整的统计表.根据图表信息,解答下列问题:
频率分布表
阅读时间 (小时) | 频数 (人) | 频率 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
合计 |
|
|
频数分布直方图
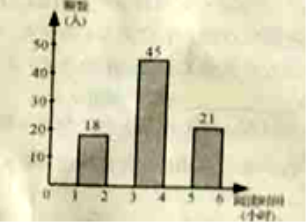
(1)填空:![]() ,
,![]() ,
,![]() ,
,![]() ;
;
(2)将频数分布直方图补充完整(画图后请标注相应的频数);
(3)若该校由![]() 名学生,请根据上述调查结果,估算该校学生一周的课外阅读时间不足三小时的人数.
名学生,请根据上述调查结果,估算该校学生一周的课外阅读时间不足三小时的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
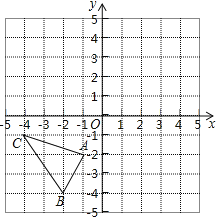
【题目】如图,在平面直角坐标系中,△ABC的三个顶点分别为A(﹣1,﹣2),B(﹣2,﹣4),C(﹣4,﹣1).
(1)把△ABC向上平移3个单位后得到△A1B1C1,请画出△A1B1C1并写出点B1的坐标;
(2)已知点A与点A2(2,1)关于直线l成轴对称,请画出直线l及△ABC关于直线l对称的△A2B2C2,并直接写出直线l的函数解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次体育达标测试中,九年级(2)班15名男生的引体向上成绩如下表:问这15名男生的引体向上成绩的中位数和众数分别是( )
成绩/个 | 8 | 9 | 11 | 12 | 13 | 15 |
人数 | 1 | 2 | 3 | 4 | 3 | 2 |
A.12,13B.12,12C.11,12D.3,4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图甲,直线y=﹣x+3与x轴、y轴分别交于点B、点C,经过B、C两点的抛物线y=x2+bx+c与x轴的另一个交点为A,顶点为P.
(1)求该抛物线的解析式;
(2)在该抛物线的对称轴上是否存在点M,使以C,P,M为顶点的三角形为等腰三角形?若存在,请直接写出所符合条件的点M的坐标;若不存在,请说明理由;
(3)当0<x<3时,在抛物线上求一点E,使△CBE的面积有最大值(图乙、丙供画图探究).

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com