
【题目】在数轴上,点M、N表示的数分别为a、b,我们把a、b之差的绝对值叫做点M、N之间的距离,即MN=│a-b│.已知数轴上三点A、O、B表示的数分别为-3,0,1,点P为数轴上任意一点,其表示的数为x.
![]()
(1)如果点P到点A、点B的距离相等,那么x=_______;
(2)当x是多少时,点P到点A、点B的距离之和是6;
(3)若点P以每秒3个单位长度的速度从点O沿着数轴的负方向运动时,点E以每秒1个单位长度的速度从点A沿着数轴的负方向运动,点F以每秒4个单位长度的速度从点B沿着数轴的负方向运动,且三个点同时出发,那么运动几秒时,点P到点E、点F的距离相等.
【答案】(1)-1;(2)x=-4或2;(3)运动![]() 秒或2秒时,点P到点E、点F的距离相等.
秒或2秒时,点P到点E、点F的距离相等.
【解析】
(1)根据三点A,O,B对应的数,得出AB的中点为:x=(-3+1)÷2进而求出即可;
(2)根据P点在A点左侧或在B点右侧分别列方程求解即可;
(3)设运动时间为t,分别表示出点P、E、F所表示的数,然后根据两点间的距离的表示列出绝对值方程,然后求解即可.
解:(1)∵A,O,B对应的数分别为-3,0,1,点P到点A,点B的距离相等,
∴x的值是-1.
故答案为:-1;
(2)存在符合题意的点P,
当P在A在左侧时,(1-x)+(-3-x)=6,解得x=-4;
当P在B在右侧时,(x-1)+[x-(-3)6,解得x=2.
∴x=-4或2.
(3)设运动时间为t,点P表示的数为-3t,点E表示的数为-3-t,点F表示的数为1-4t,
∵点P到点E,点F的距离相等,
∴|-3t-(-3-t)|=|-3t-(1-4t)|,
∴-2t+3=t-1或-2t+3=1-t,
解得t=![]() 或t=2.
或t=2.
答:运动![]() 秒或2秒时,点P到点E、点F的距离相等.
秒或2秒时,点P到点E、点F的距离相等.


 春雨教育同步作文系列答案
春雨教育同步作文系列答案科目:初中数学 来源: 题型:
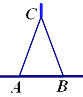
【题目】小知识:如图,我们称两臂长度相等(即![]() )的圆规为等臂圆规. 当等臂圆规的两脚摆放在一条直线上时,若张角
)的圆规为等臂圆规. 当等臂圆规的两脚摆放在一条直线上时,若张角![]() ,则底角
,则底角![]() .
.
请运用上述知识解决问题:
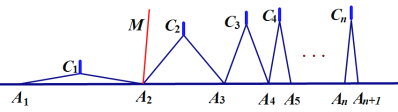
如图,![]() 个相同规格的等臂圆规的两脚依次摆放在同一条直线上,其张角度数变化如下:
个相同规格的等臂圆规的两脚依次摆放在同一条直线上,其张角度数变化如下:
![]() ,
,![]() ,
, ![]() ,
,![]() ,…
,…
(1)、①由题意可得![]() = ;
= ;
②若![]() 平分
平分![]() ,则
,则![]() = ;
= ;
(2)、![]() = (用含
= (用含![]() 的代数式表示);
的代数式表示);
(3)、当![]() 时,设
时,设![]() 的度数为
的度数为![]() ,
,![]() 的角平分线
的角平分线![]() 与
与![]() 构成的角的度数为
构成的角的度数为![]() ,那么
,那么![]() 与
与![]() 之间的等量关系是 ,请说明理由. (提示:可以借助下面的局部示意图)
之间的等量关系是 ,请说明理由. (提示:可以借助下面的局部示意图)
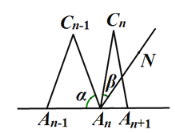
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD为平行四边形,∠BAD的角平分线AE交CD于点F,交BC的延长线于点E.
(1)求证:BE=CD;
(2)连接BF,若BF⊥AE,∠BEA=60°,AB=4,求平行四边形ABCD的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们约定:对角线相等的四边形称之为:“等线四边形”。
(1)①在“平行四边形、菱形、矩形、正方形”中一定是“等线四边形”的是___________________;
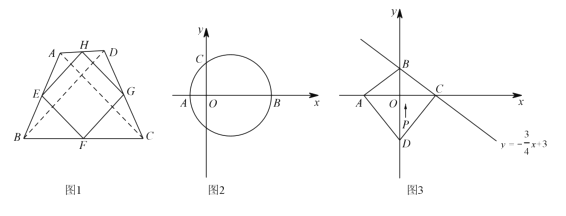
②如图1,若四边形![]() 是“等线四边形”,
是“等线四边形”, ![]() 分别是边
分别是边![]() 的中点,依次连接
的中点,依次连接![]() ,得到四边形
,得到四边形![]() ,请判断四边形
,请判断四边形![]() 的形状:______________________;
的形状:______________________;
(2)如图2,在平面直角坐标系![]() 中,已知
中,已知![]() ,以
,以![]() 为直径作圆,该圆与
为直径作圆,该圆与![]() 轴的正半轴交于点
轴的正半轴交于点![]() ,若
,若![]() 为坐标系中一动点,且四边形
为坐标系中一动点,且四边形![]() 为“等线四边形”。当
为“等线四边形”。当![]() 的长度最短时,求经过
的长度最短时,求经过![]() 三点的抛物线的解析式;
三点的抛物线的解析式;
(3)如图3,在平面直角坐标系![]() 中,四边形
中,四边形![]() 是“等线四边形”,
是“等线四边形”, ![]() 在
在![]() 轴的负半轴上,
轴的负半轴上,![]() 在
在![]() 轴的负半轴上,且
轴的负半轴上,且![]() 。点
。点![]() 分别是一次函数
分别是一次函数![]() 与
与![]() 轴,
轴,![]() 轴的交点,动点
轴的交点,动点![]() 从点
从点![]() 开始沿
开始沿![]() 轴的正方向运动,运动的速度为2个单位长度/秒,设运动的时间为
轴的正方向运动,运动的速度为2个单位长度/秒,设运动的时间为![]() 秒,以
秒,以![]() 点为圆心,半径
点为圆心,半径![]() ,单位长度作圆,问:①当
,单位长度作圆,问:①当![]() 与直线
与直线![]() 初次相切时,求此时运动的时间
初次相切时,求此时运动的时间![]() ;②当运动的时间
;②当运动的时间![]() 满足
满足![]() 且
且![]() 时,
时,![]() 与直线
与直线![]() 相交于
相交于![]() ,求弦长
,求弦长![]() 的最大值。
的最大值。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=x2+bx+c与x轴交于A,B两点,且点A在点B的左侧,直线y=﹣x﹣1与抛物线交于A,C两点,其中点C的横坐标为2.
(1)求二次函数的解析式;
(2)P是线段AC上的一个动点,过点P作y轴的平行线交抛物线于点E,求线段PE长度的最大值.

查看答案和解析>>
科目:初中数学 来源: 题型:
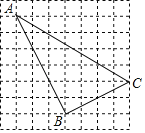
【题目】已知图中的每个方格都是边长为1的小正方形,每个小正方形的顶点称为格点,△ABC的顶点在格点上,称为格点三角形,请按要求完成下列各题
(1)填空:
AB= ,BC= ,AC= ;
(2)试判断△ABC的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于任意四个有理数a,b,c,d,可以组成两个有理数对(a,b)与(c,d).我们规定:
(a,b)★(c,d)=bc-ad.
例如:(1,2)★(3,4)=2×3-1×4=2.
根据上述规定解决下列问题:
(1)有理数对(2,-3)★(3,-2)=_______;
(2)若有理数对(-3,2x-1)★(1,x+1)=7,则x=_______;
(3)当满足等式(-3,2x-1)★(k,x+k)=5+2k的x是整数时,求整数k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在大课间活动中,体育老师随机抽取了七年级甲、乙两班部分女学生进行仰卧起坐的测试,并对成绩进行统计分析,绘制了频数分布表和统计图,请你根据图表中的信息完成下列问题:
分 组 | 频数 | 频率 |
第一组(0≤x<15) | 3 | 0.15 |
第二组(15≤x<30) | 6 | a |
第三组(30≤x<45) | 7 | 0.35 |
第四组(45≤x<60) | b | 0.20 |
(1)频数分布表中a=_____,b=_____,并将统计图补充完整;
(2)如果该校七年级共有女生180人,估计仰卧起坐能够一分钟完成30或30次以上的女学生有多少人?
(3)已知第一组中只有一个甲班学生,第四组中只有一个乙班学生,老师随机从这两个组中各选一名学生谈心得体会,则所选两人正好都是甲班学生的概率是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校组织七、八年级全体同学参观八路军太行纪念馆(位于山西省长治市武乡县城).七年级租用45座大巴车![]() 辆,55座大巴车
辆,55座大巴车![]() 辆;八年级租用30座中巴车
辆;八年级租用30座中巴车![]() 辆,55座大巴车
辆,55座大巴车![]() 辆.当每辆车恰好坐满时:
辆.当每辆车恰好坐满时:

(1)用含有![]() ,
,![]() 的代数式分别表示七、八年级各有学生数.
的代数式分别表示七、八年级各有学生数.
(2)用含有![]() ,
,![]() 的代数式表示七、八年级共有多少学生?
的代数式表示七、八年级共有多少学生?
(3)当![]() ,
,![]() 时,该学校七、八年级共有多少学生?
时,该学校七、八年级共有多少学生?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com